Diffusion equations for early stages of solid solutions decay based on the Markovian theory of random walk

We have examined the early stages of binodal or spinodal solid solutions decay connected with the growth of local zones of concentration`s inhomogeneities (clusters) that initially appeared like concentration fluctuations. The particles transport with short diffusion paths that cause the growth of the clusters can be correctly described by theory of Markovian process of random walk of the individual atoms. Having decomposed Chapman-Kolmogorov equation for discrete random jumps of impurity atoms in a series of small parameters Δx (lattice parameter) and Δt (jump time) in one-dimensional case we have obtained a non-stationary equation of elliptic type , where α – jump probability (depends on concentrations, temperature, etc.), P – probability of finding the specific atom in lattice site. For the dependence of α(P) in the parabolic approximation provided that , the resulting equation predicts the growth of concentration’s inhomogeneities and transformation of initial concentration fluctuations into growing clusters with surface boundary, as demonstrated by numerical calculation (Fig.1). Taking into account the last term in the equation we obtain quasiperiodic concentration distribution inherent in spinodal decomposition (Fig.2).

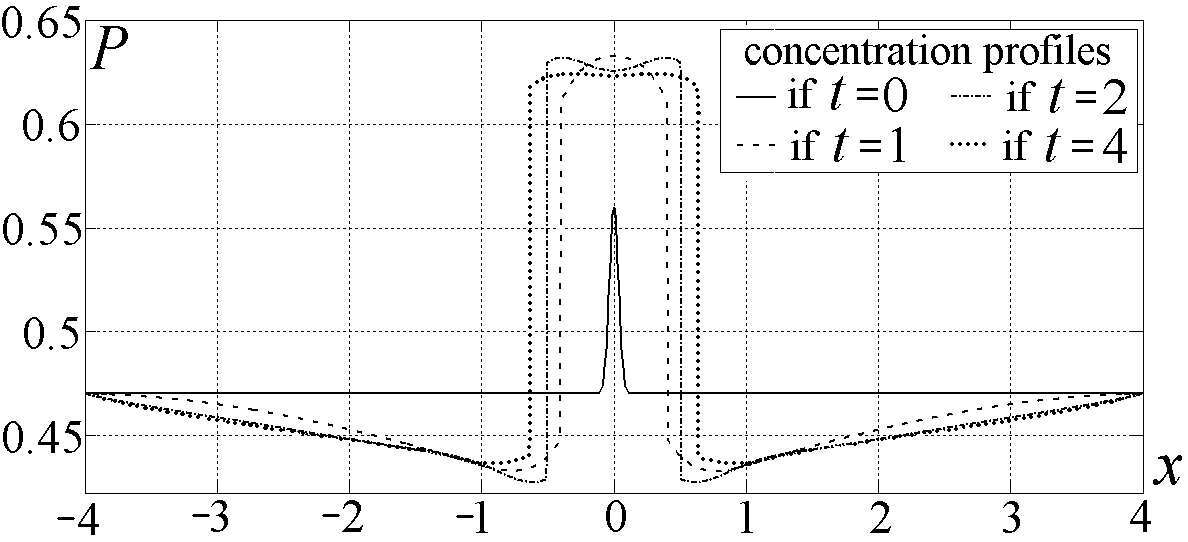
Fig. 1 Fig. 2

The work was supported by RFBR grant 16-42-710770.