Spectral Resolution Improvement by Waveform Estimation Methods

Introduction: Scintillator based radiation detectors frequently measure spectra in electromagnetically noisy environment. In this work, spectra resolution improvement of various algorithms evaluated in a simulated noisy environment. Internal power convertors and external devices, such as cell phones, are a few of the noise sources that reduce detector`s performance. Analog filters and pulse shaping are common solutions, however, are less effective in reducing digital noises (delta type noises) and errors introduces by low rate sampling.

This work proposes a suitable algorithm, for implementation on limited performance microcontroller imbedded in a mobile handheld device. Performance evaluation of the algorithms is based on complexity, spectra resolution and rejection rate.

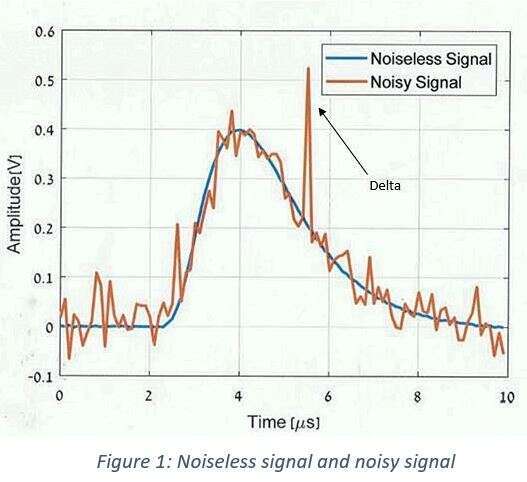
Methods: Gaussian distributed noise and a delta type noise were added to characterize the real environment, see Fig. 1. The model can be written as follows:

x[n] = α·s[n]+v[n], n=1,2,...,N.

s[n] – Input signal without noise.

v[n] – Additive noises.

x[n] – Noisy signal.

α – The unknown parameter to be estimated.

2.1 Peak Detector

Common method of pulse height estimation is simply measuring the maximal value, which might result in sampling the delta noise instead of the actual signal maximum, see Fig. 1. Such noise sampling is solved by somewhat more sophisticated median class computation of the peak. However, for Gaussian noise this method is less effective.

2.2 Polynomial Estimation

Least Squares^[1] (LS) method is used to fit a polynomial function to the input signal using a few coefficients. LS requires matrix inversion, which greatly increases the algorithm`s complexity. Polynomial estimation, for high number of samples, yields the highest spectra resolution improvement. However, in some cases, including samples of the non-polynomial edges severely degrades estimation. Consequently, complex roots and maximum value out of range cause rejection of an event.

2.3 Correlation Estimation

Time of maximum signal correlation is found by overlapping of noiseless and noisy signals. Afterwards, the noisy signal`s amplitude is estimated by an Efficient Estimator^[2]. The efficient estimator is unbiased and characterized with minimum variance among all unbiased estimators.

Results: Selection of the best method depends on required application characteristics; among those are noise`s type and level, memory capacity and sampling rate of the microcontroller and the total complexity of the algorithm.

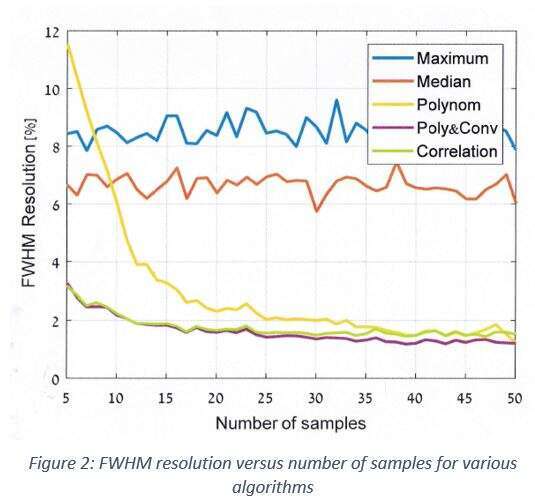
It can be observed from Fig. 2 that Polynomial and Correlation estimation methods outperform less sophisticated methods described in Section 2.1. The advantages of the Correlation method are the algorithm`s low complexity and zero rejection rate. Polynomial estimation provides the best resolution of compared methods, but introduces a rejection rate, which can be avoided by taking a lower number of samples with minor decrease in performance. Therefore, for limited computation power devices, the Correlation method is the prime choice due to low complexity and near Polynomial`s method performance.