Invited
Non-linear Dynamics, Chaos and Synchronization of Optomechanical Crystal Cavities

Nonlinear dynamics is a branch of physics that studies systems described by equations more complex than the linear form. Nonlinear systems, such as the weather or neurons, often appear chaotic, unpredictable or counterintuitive, and yet their behaviour is deterministic. In this work we report on various dynamical states achieved in Si-based optomechanical crystal cavities (OMCs) derived from typical optical nonlinearities of Si, which include the optomechanical interaction with mechanical eigenmodes supported by the system [1].

For a given wavelength and power in the cavity, the dynamical solution of the OMC can be a self-sustained oscillation called self-pulsing that modulates light in a coherent way. When a harmonic of the main frequency of the self-pulsing is resonant with a mechanical mode there is a strong amplification of the motion leading to a “mechanical lasing” regime. If the number of photons is large enough, the dynamics of the system became increasingly complex and evolve towards a period-doubling cycle and finally chaos [2].

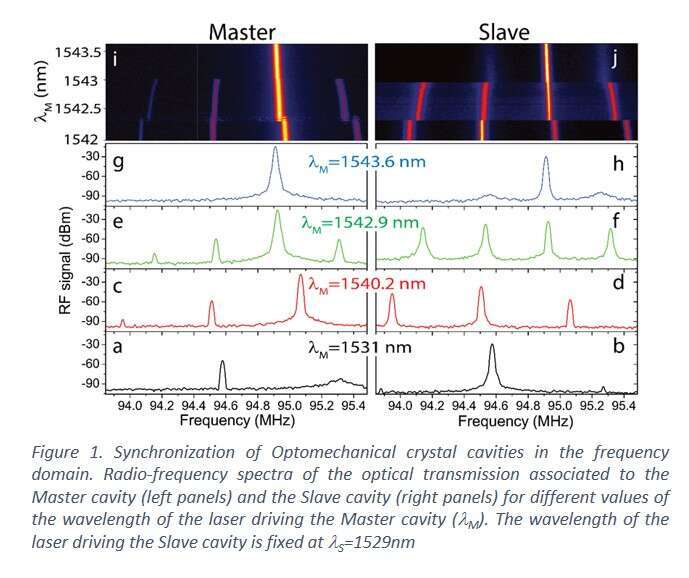
Our studies are extended to a pair of two OMCs connected by a small mechanical link and completely isolated optically. We demonstrate mechanical synchronization of the two OMCs (Figure 1), satisfying all the requirements of the synchronization definition [3]. Simultaneous recording of the optical transmission temporal traces of each of the two cavities allows concluding that, in the synchronized state, they mechanically oscillate in anti-phase, which is in agreement with the predictions of our numerical model. Finally, we demonstrate that, when the coupled system is in a synchronized state, it is possible to disable it while actuating over one of the cavities with a heating laser, so that both cavities oscillate independently.

These results are the first step towards building networks of weakly coupled OMCs able to display collective dynamics susceptible to be modified by addressing single structures with external perturbations, thus enhancing the performances of single nano-mechanical oscillator systems and constituting a novel architecture for neuromorphic computing applications.

[1] D. Navarro-Urrios et al., Sci. Rep. 5(1), 15733 (2015).

[2] D. Navarro-Urrios et al., Nat. Commun. 8, 14965 (2017).

[3] M. F. Colombano et al., arXiv:1810.06085 (2018).

Contact e-mail: dnavarro@ub.edu