ON THE IMPORTANCE OF VARIABILITY WHEN MANAGING METROLOGY CAPACITY

In a former publication we formalize a problem for a manufacturing cell where a unique metrology tool controls several heterogeneous production machines. An approach is proposed to determine the sampling periods (the number of products produced between two consecutive inspections) for the different production machines such as to minimize the expected product scrap or rework rate. Production machines are characterized by their failure rate, their throughput rate, and their consumption of the metrology capacity. The resulting problem can be formulated as an optimization problem where the goal is to minimize the expected product loss happening between the machine failure and its detection, subject to the constraint of the metrology capacity, the decision variables being the sampling periods of production machines. The problem was reformulated as a Multiple-Choice Knapsack Problem (MCKP), for which we proposed several heuristics based on the work of Sinha and Zoltners (1979) and Pisinger (1995).

In this former body of work, the assumption was made of an immediate answer from the metrology tool, and that production can be synchronized with metrology, and thus that metrology capacity can be fully exploited. More often than not, this is not the case. We now consider that a queue is forming at the metrology tool that delays its response (see Figure 1).

The expected sojourn time of lots sent to metrology is given by Kingman`s approximation (see Kingman (1962)) for G/G/1 queues.

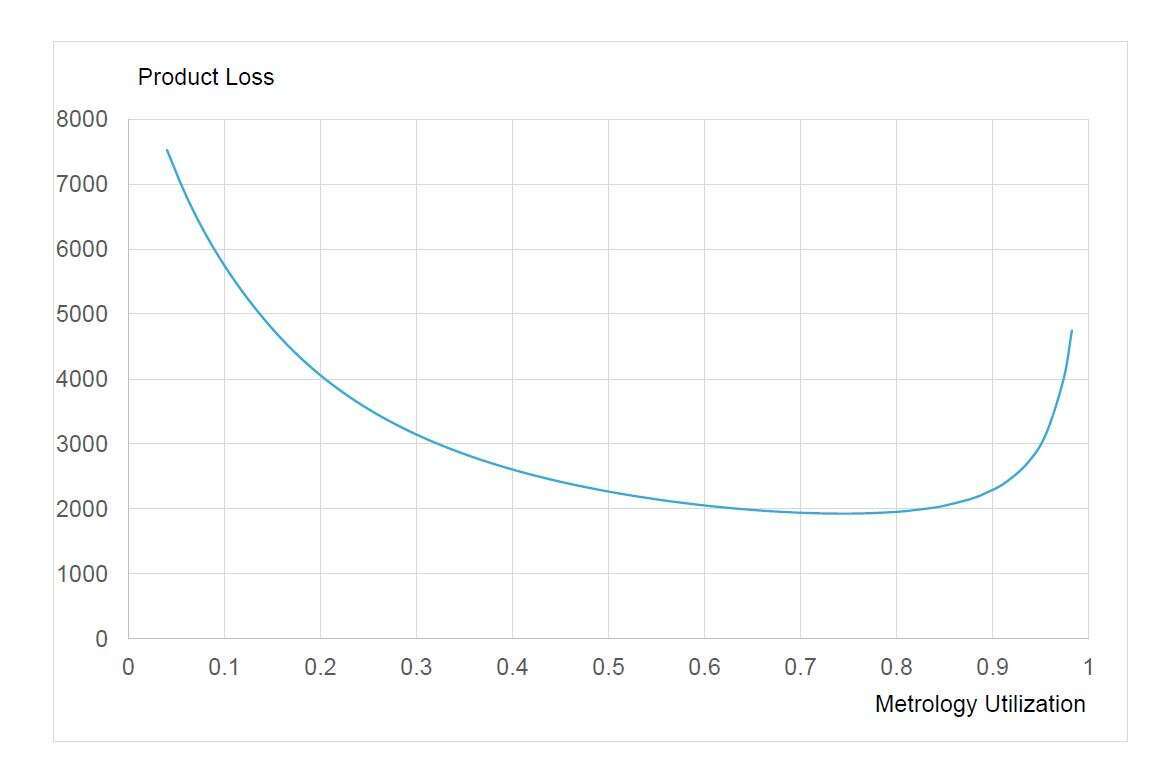
In an environment where no synchronization is possible between the metrology availability and the arrival of products to be measured, the expression of the Product Loss shows that there is a trade-off between the benefits associated with decreasing the sampling periods of the different production machines and the product loss due to the resulting waiting at the metrology tool (Figure 2).

We simplify the problem by hierarchically considering the questions of the right level of utilization for the metrology tool and of the sampling period for each production machine.

Our approach iteratively uses the solution of a modified version of the Integer Linear Program solved in Dauzere-Peres et al. (2016).

Following this formulation, we present an algorithm aimed at solving the ILP. The heuristic results are analyzed over a large number of scenarios by using a regression tree for the adequate level of utilization while the scenario characteristics, namely the machine reliability, production rate, measurement rate relative to the production rate, and the variability factor were defined as potential predictors. The number of machines and the level of variability appear as the main contributors to the prediction model which allow us to provide the simple recommendations about the correct level of metrology utilization presented in Table 1