Translational covariance of flexoelectricity at ferroelectric domain walls

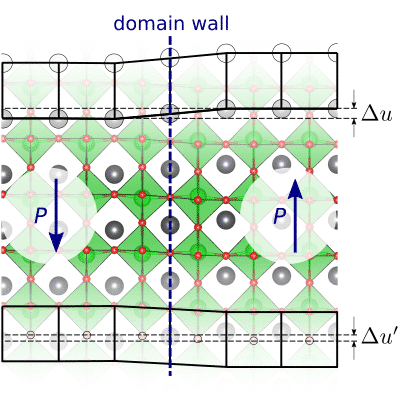
Macroscopic descriptions of ferroelectrics have an obvious appeal in terms of efficiency and physicalintuition. Their predictive power, however, has often been thwarted by the lack of a systematic procedureto extract the relevant materials parameters from the microscopics. Here we address this limitation byestablishin an unambiguous two-way mapping between spatially inhomogeneous fields and discretelattice modes. This yields a natural treatment of gradient couplings in the macroscopic regime via a long-wavelength expansion of the crystal Hamiltonian. Our analysis reveals an inherent arbitrariness in both theflexoelectric and polarization gradient coefficients, which we ascribe to a translational freedom in thedefinition of the polar distortion pattern. Remarkably, such arbitrariness cancels out in all physicallymeasurable properties (relaxed atomic structure and energetics) derived from the model, pointing to ageneralized translational covariance in the continuum description of inhomogeneous ferroelectricstructures. We demonstrate our claims with extensive numerical tests on 180° domain walls in commonferroelectric perovskites, finding excellent agreement between the continuum model and direct first-principles calculations.