When supersonic flow conditions are imposed over slender bodies in close proximity, aerodynamic interference effects precipitates between the bodies. The bow-shock wave and forebody expansion field produced by an adjacent body (the disturbance generator) impinge onto the body of interest (the disturbance receiver), which reorganises its surface-flow topology and modifies its surface pressure distribution, effectively altering its nominal centre of pressure and overall aerodynamic behaviour. The mutual bow-shock interaction has increased complexity due to the multiple shock wave reflections, shock diffraction and viscous shock wave interactions manifesting within the interference domain. Moreover, when the receiver body is at an incidence setting relative to the supersonic freestream, strong vortices dominate the receiver’s leeward region, implying that the viscous shock interactions are not just limited to the boundary-layer flow over the body of interest, but generate shock-vortex interactions as well.
Previous research under the topic of aerodynamic interference has led to several publications, which may be categorised under two main research areas: The first category of research was aimed at quantifying the change in aerodynamic forces and moments experienced by the body of interest within the disturbance flowfield [1-2], and the second focused on the body’s surface pressure distribution and near-surface flow topologies [3-4]. Many of these researchers have reported that the complex interference flowfield is bespoke to each configuration, yet, very little or no information is available in open literature with the body of interest at angles of sideslip relative to the generator body, where complete, three-dimensional flow asymmetry exists. Understanding the underlying flow physics, the compression wave topology surrounding the receiver, and the viscous shock interactions produced with the disturbance receiver at large angles of sideslip relative to the generator is the primary focus of this paper. The current study employs an experimentally validated computational technique to investigate the bow-shock interactions generated between the bodies. Due to the asymmetric arrangement of the dual slender body configuration, the numerical simulations allow the finer details of the interaction to be studied, which would otherwise require very elaborate experimental flow diagnostic techniques, or may be overlooked by traditional methods completely.
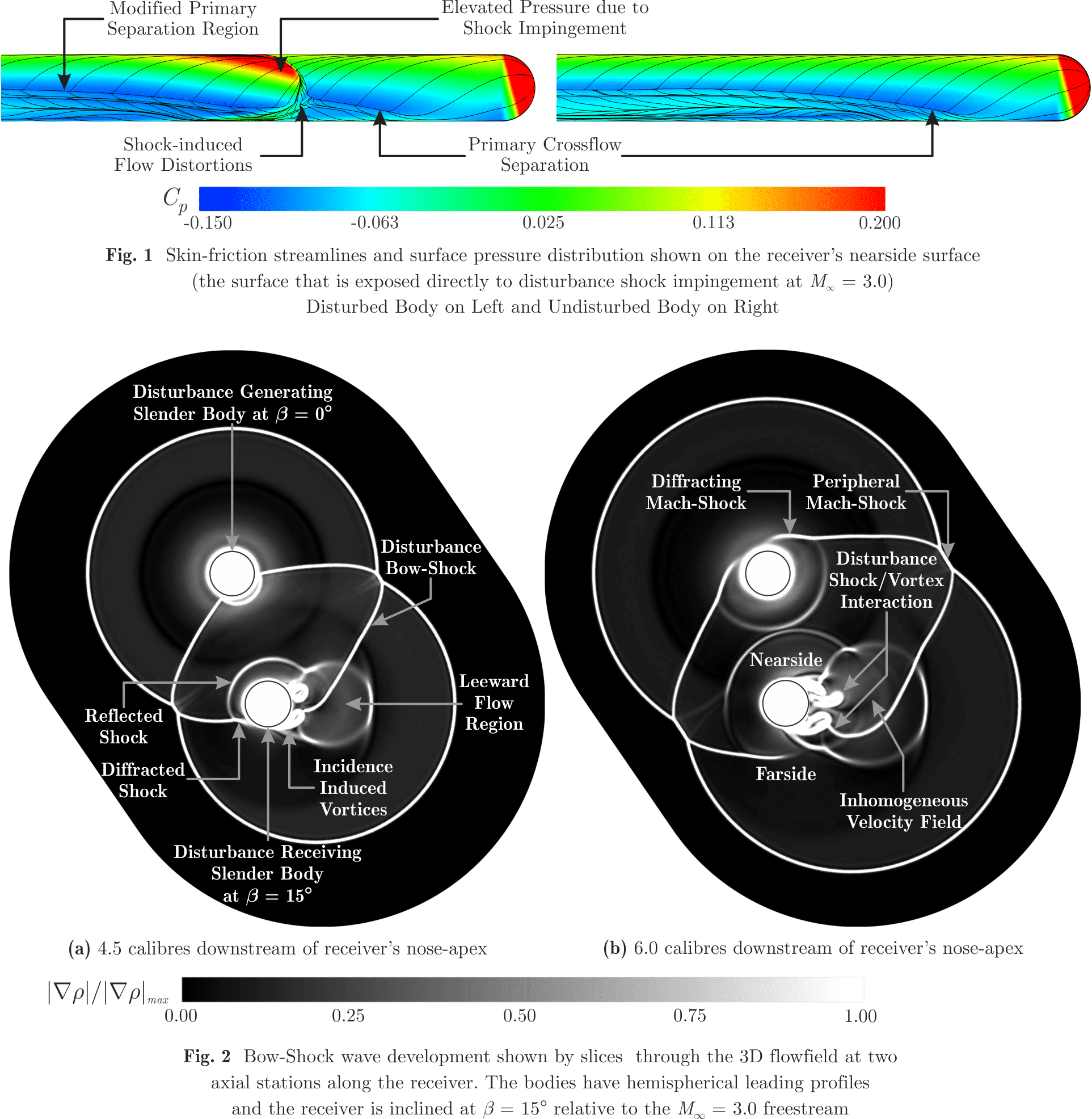
To demonstrate the complexity of the interaction, the surface pressure distribution developed over the receiver body is compared to that produced by an equivalent undisturbed body in Fig. 1, with the wave system generated in the three-dimensional flowfield shown in Fig. 2. Not only does the disturbance shock induce local elevations in pressure on the disturbed receiver’s surface, but it also alters the nominal trajectory of the separation and reattachment regions developed over the body. Moreover, as the disturbance bow-shock strikes the receiver, a portion of the wave is reflected back towards the generator in the inter-model region, while the residual portion of the wave diffracts over the body and progresses to the receiver’s farside region. During passage, the diffracting disturbance wave induces severe effects of compressibility onto the receiver’s incidence-induced body-vortices, while the inhomogeneous velocity field in the recirculation region alters the disturbance wave’s curvature and tempers its propagation through the flowfield. Although the mechanics of the interaction are not yet fully understood, multiple shock reflections, Mach reflections, as well as shock-induced separation and shock-induced vortex-shedding are among the rich phenomena produced by this three-dimensional bow-shock interaction.
References
[1] Wilcox, F (1995) Separation Characteristics of Generic Stores from Lee Side of an Inclined Flat Plate at Mach 6. NASA Technical Memorandum 4652.
[2] Chaplin R, MacManus D, Birch, T (2010) Aerodynamic interference between high-speed slender bodies. Shock Waves, 20, 467-482.
[3] Brosh, A, Kussoy, M, Hung, C (1985) Experimental and numerical investigation of a shock wave impingement on a cylinder. AIAA J. 23(6), 840–846.
[4] Mowatt S, Skews B.W (2011) Three-Dimensional Shock Wave/Boundary Layer Interactions. Shock Waves, 21, 89-101.
Figures