When a planar shock wave encounters a straight wedge, the reflection configuration is either an irregular or regular reflection. Which of these configurations occurs may be predicted from the Mach number and angle of incidence between the shock wave and the wedge. When a shock wave is curved, both the Mach number and incidence angle vary as the shock propagates along the wedge, and the resulting reflection may change configuration during the reflection process.
Itoh et. al. [1] describe a method for predicting the transition from Mach reflection (MR) to regular reflection (RR) for planar shock waves encountering a concave cylindrical surface. The method involves using geometry to derive an expression for the Mach stem height as a function of the ratio of the Mach numbers of the incident shock and Mach stem, which are estimated by applying Whitham`s theory [2]. Integrating the resulting expression gives a prediction for the triple point trajectory. The point at which the triple point trajectory crosses the reflection surface may be used to predict the transition from MR to transitioned regular reflection (TRR).
The current paper applies a similar approach to obtain an approximate triple point trajectory of the MR of a converging cylindrical shock segment encountering a straight wedge. This also allows estimation of the point at which the MR-TRR transition occurs.
Experiments were carried out for wedges 72 mm in length, and at angles between 15° and 50° and cylindrical shock segments with Mach numbers varying between 1.52 and 2.08 at the wedge apex, with radii between 110 and 125 mm. The resulting reflection patterns were captured using a high speed camera. A schlieren photograph of a Mach 1.55 shock and a 25° wedge is shown in Fig. 1.
Fig. 2 compares the triple point trajectories predicted by the model to those obtained in the experiments. The model is most accurate for the 30° wedge, giving a reasonable approximation of the Mach stem height, and predicting the MR-TRR transition point to within 5% of the wedge length for all Mach numbers tested. For wedges inclined at 40° or more, the transition point was overestimated by between 10% and 20%, and the predicted Mach stem height is significantly overestimated. For the 15° wedge, there was reasonable agreement between the predicted triple point trajectory and that obtained in the experiments, and there was close agreement for the maximum height of the Mach stem. However, the shock wave reached the end of the wedge before transition to TRR took place, so no comparison of the transition point could be made for this angle.
The overestimation of the trajectory for steeper wedge angles is likely caused by the fact that the model does predict a triple point trajectory for all wedge angles, even those for which the initial reflection falls within the RR domain. Another limitation of the model is that it assumes that the Mach stem is straight and perpendicular to the wedge, but the Mach stems observed were slightly curved, and began to tilt significantly as they approached the transition point.
However, the model does provide reasonable approximations of the triple point trajectories and MR-TRR transition points for shock waves of moderate strength for wedge angles below 40°.
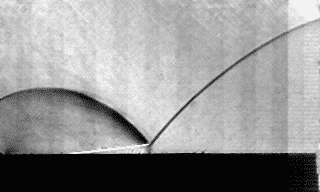
Figure 1 - Schlieren photograph of a Mach 1.55 converging cylindrical shock reflecting off a 25° wedge
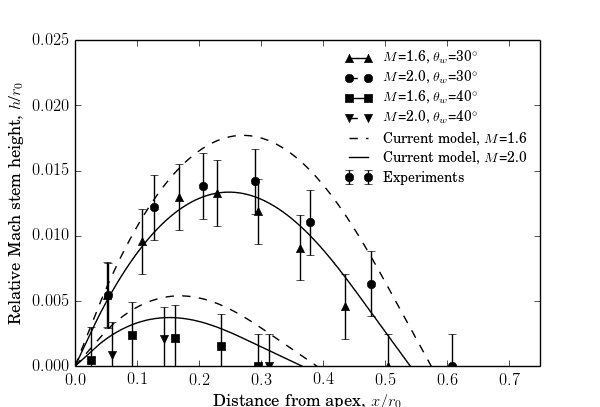
Figure 2 - Comparison between predicted triple point trajectories and those obtained in experiments
References:
1. Itoh S, Okazaki N, and Itaya M (1981) On the transition between regular and Mach reflection in truly non-stationary flows. J Fluid Mech 108:383--400.
2. Whitham GB (1957) A new approach to problems of shock dynamics, Part I: Two-dimensional problems. J Fluid Mech 2:145--171.

