The formation of Mach waves from supersonic jets with outer coflowing

A supersonic free jet can emit shock waves to the outside environment as well as to the inside of the jet. These shock waves are commonly called "Mach waves" and have been known for many decades. For a long time it has also been well known that a surrounding secondary coflowing jet can diminish the primary jet noise exerted by the Mach waves to the outer atmosphere. This noise reduction is important for the jet engines of airplanes and other noisy supersonic jet devices. Other applications with a jet envelope are e.g. burners, cutting torches and oxygen injection systems in the steel industry. Numerous scientists have studied this phenomenon in detail, among others, Papamoschou & Roshko [1], Papamoschou [2] and Rossman et al. [3]. Oertel [4] carried out many experiments with supersonic free jets surrounded by a subsonic coflowing envelope. These experiments showed that by reasonably adapted secondary-jet conditions the Mach waves can be largely suppressed. Based on the theory of Oertel sen. et al. [5] for describing the Mach wave dynamics of a simple supersonic jet, extended relations were derived for the case with infinite outer coflowing. This theory begins with the well known Kelvin-Helmholtz-instabilities (KHI) which appear when sound waves and other disturbances cause the nozzle boundary layer to become unstable as it leaves the nozzle exit to form the jet’s mixing layer. As described by Oertel sen. et al. [5], if Mach waves exist, the KHI break into two vortices which move stably downstream in two separate vortex train rows with generally different vortex spacing. The vortex velocities are w’ and w’’ with w’ > w’’, and the mean velocity w. Figure 1 schematically shows a section of the mixing layer with the two vortex trains. In this figure, the two vortex trains are drawn with the same thickness, which is only the case of identical sound speeds a_i in the jet and a_a in the outer part.

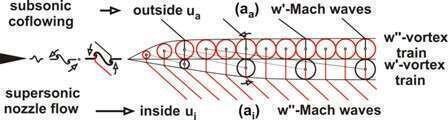
Fig. 1: Two vortex trains inside the mixing layer

The equations of Oertel sen. et al. [5] for a simple jet are extended to the coflowing dual-jet case. These result in engineering formulae for calculating the velocities w, w’ and w’’ and the Mach angles α, α’ and α’’. By gasdynamic considerations on the vortex existence stability inside the mixing layer, the following formulae with M_i the jet’s Mach number and M_a the coflowing jet Mach number have been derived. The relations (1) – (3) depend only on M_i and M_a as well as on the speeds of sound outside and inside the jet: a_a and a_i.

(1) w/a_a = (M_i + M_a)/(1+ a_a/a_i) = 1/ sin α,

(2) (w’–u_a)/a_a = ((M_i + w/a_a)/(1+ a_a/a_i)) – M_a = 1/sin α’,

(3) (u_i–w’’)/a_i = M_i – ((M_a + w/a_i)/(1+ a_i/a_a)) = 1/ sin α’’.

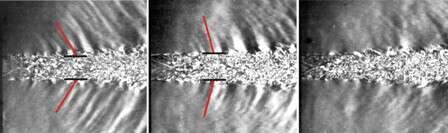
Fig. 2: Air jet at M_i = 2 with outer coflowing: a) M_a = 0, b) M_a = 0.17, c) M_a = 0.23

The derivation of the theoretical relations (1) – (3) is explained and its quality is confirmed by some examples from the literature. For example Fig. 2 [4] shows, from left to right a series of Mach number M_i = 2 air jets: a) without coflowing, b) with M_a = 0.17 and c) with M_a = 0.23. The ratio a_a/a_i of the sound velocities is: 2a) 1.40, 2b) 1.41 and 2c) 1.44. According to formula (2) the outer Mach wave angle for Fig. 2a is: α’ = 58° and for Fig. 2b it is: 76°. For (w’–u_a)/a_a < 1 no w’-Mach waves should exist, which is the case for Fig. 2c with (w’–u_a)/a_a = 0.96. In Figs. 2a-c, one can see that the statements derived from the formulae (1) and (2) are well met. The angles of the Mach waves in Fig. 2a agree quite well with the calculated one of 58°, marked as red lines. The Mach waves in Fig. 2b are steeper than in Fig. 2a and also fit the predicted Mach angle quite well. The theoretically predicted Mach wave suppression is practically fulfilled too as seen in Fig. 2c. The formulae of our theory show the limits for Mach wave suppression which is discussed for various coflowing jet conditions.

References

[1] Papamoschou D., Roshko A., The compressible turbulent shear layer: an experimental study, Journal of Fluid Mech., Vol. 197, pp. 453-477, 1988

[2] Papamoschou D., Linear model of Mach wave suppression in a dual-stream jet, AIAA 2000-2062, 2000

[3] Rossmann T., Mungal M. G., Hanson R. K., Character of Mach wave radiation and convection velocity estimation in supersonic shear layers, AIAA 2002-257, 2002

[4] Oertel H., Les ondes de Mach à l’intérieur et à l’extérieur du jet supersonique avec ou sans envelope subsonique, ISL report, CO 205/81, 1981

[5] Oertel H. Sen., Seiler F., Srulijes J., Visualization of Mach waves produced by a supersonic jet and theoretical explanations, Journal of Visualization, Vol. 16, Issue 4, pp. 303-312, 2013