Re–entry flights in carbon dioxide–nitrogen atmospheres such as Mars and Venus became more and more the focal point of interest in the research community lately. During these re–entry flights at hypersonic velocities a high enthalpy flow field is generated behind the bow shock. Due to this high enthalpy flow field the constituent chemical species inside this field undergo several significant real gas effects for example dissociation (Fig. 1).

Fig. 1: 10 Species equilibrium composition of a mixture of 97% CO2 and 3% N2
With respect to typical re–entry trajectories starting at high altitudes, low density/low pressure regions are passed during re–entry flights, whereby dissociation occurs at a wide range, starting at relatively low gas temperatures affecting aspects like surface chemistry or wall heat fluxes significantly. Therefore it is important to generate accurate thermodynamic, kinetic and transport models with a chemical non–equilibrium approach, where the conservation equations for momentum, total energy and balance equations are solved for each species in the dissociated flow field.
In this work a finite rate model [1] with different reactions schemes is implemented in a coupled Euler–boundary layer non equilibrium method using a 4th order central finite difference method for the shock discretization as well as a 3rd order upwind scheme and a split matrix approach to discretize the inviscid flow field accounting for all relevant species according to the reaction scheme used. Furthermore a shock fitting method is used as well as a 2nd order Runge Kutta approach for time stepping. To eliminate the numerical stiffness behind the shock “effective Rankine Hugoniot” relations have been applied using modified concentration schemes [2]. The boundary layer is discretized using a 2nd order Crank Nicolson scheme. Transport phenomena like diffusion of multi–component mixtures, derived from binary diffusion coefficients [3], viscosity or heat conductivity are modelled using collision integrals of higher order, which are based on (m,n) Lennard Jones potentials [4,5] applying the Wilke mixture rule [6]. Hypersonic flight simulations at different velocities and altitudes will be presented and compared to already available equilibrium simulations using an analogous approach [7]. As a test configuration a hyperbola/hyperboloid is used (Fig. 2).
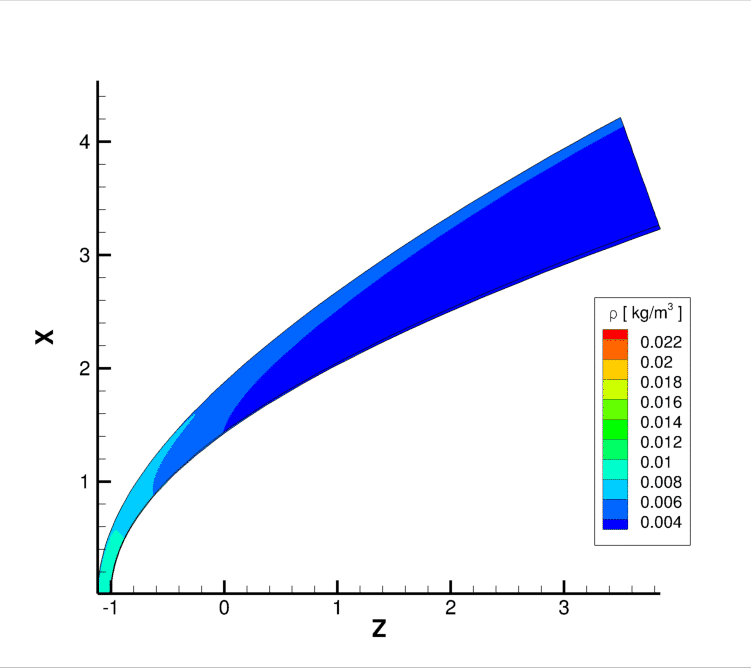
Fig. 2: Density distribution of a non-equilibrium simulation in Mars atmosphere Ma=26, altitude=38km, aoa=0.0°
The approach made here is less general than solving the Navier–Stokes equations. It solves the inviscid Euler equations first, providing the boundary conditions for the boundary layer equations. This method provides a 2nd order boundary layer solution after the first simulation cycle. Therefore 2nd order phenomena e.g. entropy layer swallowing are already taken into account. The boundary layer solution again provides an equivalent source distribution, which is used as boundary condition for the 2nd order Euler equations to simulate the displacement effect. In accordance to the theory of small disturbances the simulation cycle has to be stopped after the second simulation to preserve the parabolic character of the boundary layer equations [8].
With respect to the fact that the Navier–Stokes equations are the most comprehensive equations for continuum fluid mechanics, but still the most computational expensive ones, this approach generates results in the same order of accuracy in its domain of application with less computational effort. It has proved its applicability for blunt re–entry bodies at high angles of attack and medium to low altitudes as long as there is no strong interaction between the viscous boundary layer flow and the inviscid Euler flow [9].
References
[1] Park, Howe, Jaffe, “Review of Chemical–Kinetic Problems of Future NASA Mission, II: Mars Entries”, Journal of Thermophysics and Heat Transfer, Vol. 8, No. 1, Jan.-March 1994.
[2] Pfitzner, “A 3-D Non–Equilibrium Shock Fitting Algorithm Using Effective Rankine–Hugoniot Relations” AIAA 22nd Fluid Dynamics, Plasma Dynamics and Laser Conference”, June 1991.
[3] Obermeier, Schaber: A simple formula for multicomponent gaseous diffusion coefficients derived from mean free path theory, Int. J. Heat Mass Transfer, Vol. 20, pp. 1301-1306, 1977.
[4] Hirschfelder, Curtiss, Bird: "Molecular theory of gases and liquids" pp. 514–610, John Riley&Sons Inc., March 1964.
[5] Sacomar, Technologies for Safe and Controlled Martian Entry, SPA.2010.3.2-04, Del.Number: D6.2, Del.Title : Modelling of Transport Properties of CO2 and N2 gas mixtures, German Aerospace Center, Institute of Aerodynamics and Flow Technology, January 2012.
[6] Mundt, “Rechnerische Simulation reibungsbehafteter Strömungen im chemischen Nichtgleichgewicht”, PhD Thesis, April 1992.
[7] Starkloff, Mundt: „Accurate interpolation of state surfaces for thermodynamic properties of equilibrium carbon dioxide–nitrogen atmospheres and their implementation in a coupled Euler–boundary layer method“, 3rd International ARA Days, May 2011.
[8] van Dyke: “Pertubation methods in fluid dynamics”, The parabolic press, Stanford, 1975.
[9] Mundt, “Calculation of hypersonic, viscous, non-equilibrium flows around reentry bodies using a coupled boundary layer/Euler method”, AIAA 27th Thermophysics Conference, July 1992.

