New Modified Pekkari Model to Analyse the Aeroelastic Stability Behaviour for a Flexible Over-expanded Roket Nozzle

Fluid-Structure interaction for a flexible over-expanded rocketnozzle using the aeroelastic stability model

N.BEKKA^1,2, M.Sellam¹, A.Chpoun¹

¹Laboratoire de Mécanique et d’Energétique d’Evry LMEE, Université d’Evry Val d’Essonne, 40 rue du Pelvoux, 91020 Evry Cedex, France

²Laboratoire des Sciences Aéronautiques, Institut d’Aéronautique et des études spatiales, Université Saad Dahlab de Blida, 09130 Blida, Algérie

Abstract:

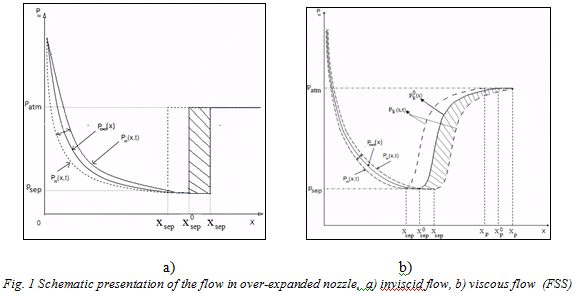
The aim and the originality of our study reside in the development of new models of aeroelastic stability called the "Modified Pekkari Model" (MPM). Inspired by the initial Pekkari model dedicated to perfect fluid flows using a simplified wall pressure distribution (Fig.1a), the new models are able to implement more complex pressure distributions associated to viscous effects (Fig.1b). This requires the introduction of a more realistic wall pressure profile for the shock separation using the free interaction theory of Chapman. To reach this objective, a structural computation code coupled with the aerodynamic excitation effects has been developed using different versions of aeroelastic stability models depending on the perfect or a viscous nature of the flow, and also on the type of stability analysis, static or dynamic.

The present study allows the computation of both natural frequencies, position of the shock separation and finally the evolution of the aeroelastic frequencies versus shock separation position. Following the analysis of Pekkari model the finite element approximation for a flexible structure when neglecting all the damping effects leads to the following system of equations:

(1)

where [M], [K] are respectively the mass and rigidity matrix, {W}, {W"} are the nodal displacements and nodal acceleration vectors respectively and {F} is the forcing vector issued from the coupling with aerodynamic loads. Namely {F} represents the instantaneous structure load due to the pressure distribution and can be given as a function of the aerodynamic rigidity matrix [K]_aero:

(2)

From physical point of view, the resultant of the aerodynamic load can be expressed as a parietal pressure difference between the equilibrium state p_w°(x) and the disturbed state pw(x,t):

(3)

Where n is the normal unit vector to the wall oriented towards to the nozzle symmety axis and w(t) represents the displacement from the equilibrium position x_sep° which has w0 as displacement. The solicitation defined by (3) allows to study the stability around an equilibrium position according to the Pekkari analysis. In general case and when the viscous effects are considered, the expression of the aerodynamic load fa(w) can be written as:

(4)

where L is the free interaction length and σ is the Heavyside function acting as a filter, defined by:

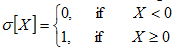
It’s clear that the corresponding expression of aerodynamic load for the initial Pekakri model can be deduced from the above generalized form of the modified model by considering a zero value of the free interaction length L:

(5)

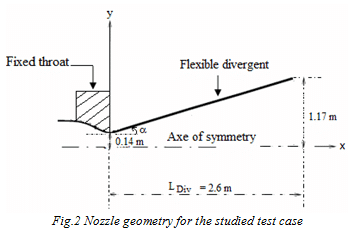
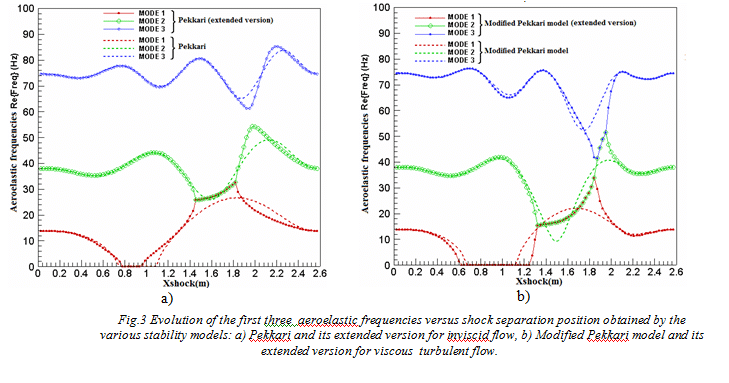
The study of the nozzle stability requires the resolution of equation (1) after writing the aerodynamic load in the framework of the finite element context using the principle of virtual works. In this paper, 2D nozzle geometry has been chosen with fixed nodes at throat and at the exit of the nozzle divergent (Fig.2). The main results are presented in a comparative manner using existing models (Pekkari and its extended version) and the modified model of Pekkari developed in this work (Fig.3). Using the modified Pekkari model, we can note that the range of static instability is relatively larger compared to that detected by the basic formulation of the initial Pekkari model. In addition, the coalescence between modes is not limited only to the first two modes and the dynamic instabilities area is relatively large compared to that detected by the extended version of the initial Pekkari model. The enlarged areas of the instability whether static or dynamic predicted by the extended version of the modified Pekkari model can be explained by the integration along an interaction length, unlike the Pekkari model where the computation of the aerodynamic load is assumed in a single node.