The limits of Mach wave emission from supersonic jets

Figure 1 shows an interference visualization taken by Oertel sen. [1] of the jet topology of Mach waves emitted towards outside and towards inside of a supersonic jet. Considerable experimental and theoretical research work was done worldwide in the past to explain the Mach wave emission phenomenon properly. Some important contributions among others, are those of Tam [2], Papamoschou [3] and Lele et al. [4]. However, although they describe the Mach wave dynamics very extensively, they do not provide a closing explanation for the mechanisms, i.e. how the Mach waves are created, how they are emitted and on what jet conditions they remain stable or not.

Fig. 1: w’- and w’’-Mach waves at Mach number M_i = 2.18, a_a/a_i = 0.95

Recently, another theory has been developed and is extensively described in the publication of Oertel sen. et al. [5]. Its central idea is the assumption that vortex pairs are formed by the rolling-up process of Kelvin-Helmholtz-instabilities taking place at the beginning of the jet’s mixing layer. If the Kelvin-Helmholtz-instabilities move supersonically they produce Mach waves, and the rolling up is interrupted by the shock/vortex interaction forming two vortex chains, as Fig. 2 depicts schematically.

Fig. 2 Vortex train model of Oertel sen. et al. [5]

The vortices move downstream within the jet boundary layer in two zones, in the inner zone with velocity w’ and in the outer one with w’’. The vortices propagating with w’, within the inner zone, produce the w’-Mach waves outside. Those vortices moving with w’’ in the outer zone initiate the w’’-Mach waves inside. The w’-vortices move faster than the w’’-vortices and form periodically vortex pairs, as they pass each other during downstream motion. Weak w-Mach waves can be produced if the overtaking manoeuvre fails and a single w-vortex is formed. Based upon gasdynamic considerations on the stability of vortices inside the mixing layer, Oertel sen. et al. [5] developed engineering formulae for calculating the velocities w, w’ and w’’ of the vortices, depending only on the jet Mach number M_i and the speed of sound of the gas outside and of the jet gas inside: a_a, respectively a_i. The relations obtained are:

(1) w/a_a = M_i / (1+ a_a/a_i),

(2) w’/a_a = (M_i + w/a_a) / (1+ a_a/a_i),

(3) w’’/a_a = (M_i - w/a_a) / (1+ a_a/a_i).

The validation of the theory was done by comparing the Mach wave angles calculated with relations (1) - (3) with flow images available from relevant publications, as e.g. [1-4], thus confirming our theory.

There exist supersonic jets which do not produce any Mach waves. This means that there must be boundaries within which Mach waves occur, and that they cannot exist outside. From our theory four limiting boundary lines, relations (4) – (7), form a region in which the Mach waves occur stably, highlighted in Fig. 3 in dark yellow and constrained above by the two red and below by the two blue boundary lines. The conditions for regular w’- and w’’-Mach waves are fulfilled only in this domain as seen for the supersonic jet in Fig. 1, see black dot in the yellow highlighted part in Fig. 3.

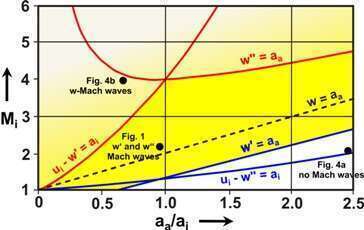
Fig. 3 Mach wave stability field

The w’- and the w’’-Mach waves can only exist at conditions where the w’- and the w’’-vortices move supersonically relative to the sound speeds outside and inside:

(4) w’ > a_a at M_i > (1 + a_a/a_i)²/(2 + a_a/a_i)

(5) u_i - w’’ > a_i at M_i > (1 + a_a/a_i)²/(1 + 2 a_a/a_i)

There are two further conditions for the vortex and Mach wave stability. Each vortex can only last if the static flow pressure sucks at each of the vortices. This happens at relative subsonic Mach numbers with

(6) w’’ < aa at M_i < (a_a/a_i)/(1 + a_a/a_i)²

(7) u_i - w’ i at M_i < (1 + a_a/a_i)²

Below the boundary lines w’ = a_a and u_i - w” = a_i no Mach waves can occur, as confirmed for the jet shown in Fig 4a. We hence call this region the "unstable subsonic region". This is a very strict condition. The transition to the region above the boundary lines w’’ = a_a and u_i – w’ = a_i, which is called the "unstable supersonic region", is smooth. If the w’- and/or the w’’- vortex chains cannot form stably in the mixing layer, a single w-vortex train may form, accompanied by w-Mach waves if the condition (8) is fulfilled. Above the dashed w-border line, as shown in Fig. 3, w-Mach waves can exist stably as confirmed by the interference jet picture shown in Fig. 4b.

(8) w > a_a at M_i > (1 + a_a/a_i)

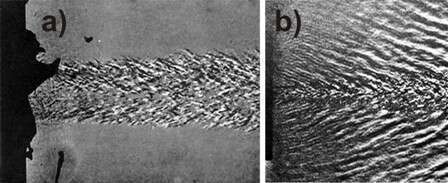
Fig. 4: a) no Mach waves at M_i = 1.98, a_a/a_i = 2.44 and b) w-Mach waves at M_i = 3.95, a_a/a_i = 0.66

References

[1] Oertel H., 33 years of research by means of shock tubes at the French-German Research Institute of Saint-Louis, Proc. 14^th International Symposium on Shock Tubes and Waves, pp. 3-13, Sydney, Archer Milton, 1983

[2] Tam C. K. W., Hu F. Q., On the three families of instability waves of high-speed jets, Journal of Fluid Mech., Vol. 201, pp. 447-484, 1989

[3] Papamoschou D., Mach wave elimination in supersonic jets, AIAA-97-0147, 1997

[4] Lele S. K., Mendez S., Ryu J., Nichols J., Shoeybi M., Moin P., Sources of high-speed jet noise: analysis of LES data and modeling, Procedia Engineering 6C, pp. 84-93, 2010

[5] Oertel sen. H., Seiler F., Srulijes J., Visualization of Mach waves produced by a supersonic jet and theoretical explanations, Journal of Visualization, Vol. 16, Issue 4, pp. 303-312, 2013