While the propagation of plane shock-waves in straight channels is well understood, their propagation in curved channels is less understood (Prasad & Parker, 2009). Even less understood is the propagation of curved shock-waves in curved channels. Solving Euler’s conservative equations for the propagation of a curved shock, while possible is computationally intensive; hence in this research we seek to implement Whitham’s theory of Geometric Shock Dynamics for a simper solution.
Edwards et al. studied the propagation of plane shocks in channels with bends of 75 mm and 150 mm, were the plane shock transforms to a curved shock and back to a plane shock. Two models were created using Whitham’s theory of shock dynamics and 3-shock theory for comparison with experiment. Whitham’s theory best described the evolution of the shock’s profile with the description becoming better as the shock’s strength was increased; on the other hand, the 3-shock theory over estimated shock velocities at the wall.
While Whitham’s theory described the profiles well, that description improved as the Mach number increased. This improved agreement at higher Mach numbers was also observed by Skews (1967) when modelling the diffraction of a plane shock around a convex corner. Observing the limitation posed by Whitham’s theory when modelling weak shocks, Milton modified the Area-Mach number (CCW) relation used in the theory as a generalisation to weak shocks (Milton, 1975).
The present research uses Whitham’s theory as modified by Milton to model the propagation of curved shocks in curved channels and verify the result by comparing the profiles so obtained with those observed from experiment. Focus is on weak shockwaves (Ms~1.5) as a means of investigating both curved shocks and the improvements, if any, that Milton’s modification has on Whitham’s theory. Figure 1, is a sketch of part of the experimental facility that will be used to investigate the curved shocks.
The test pieces that model the wall profiles were designed based on preliminary CFD studies. Figure 2 shows a CFD study that was done using ANSYS Fluent (version 15.0), for a test piece with a 150 mm radius. The curved shock is observed to transform to an almost plane shock at the channel’s throat and back to a curved shock.
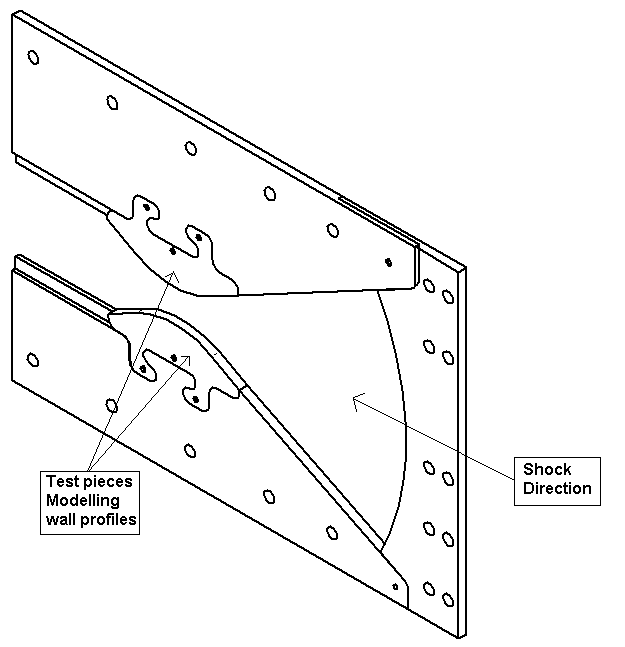
Figure 1: Sketch of experimental facility
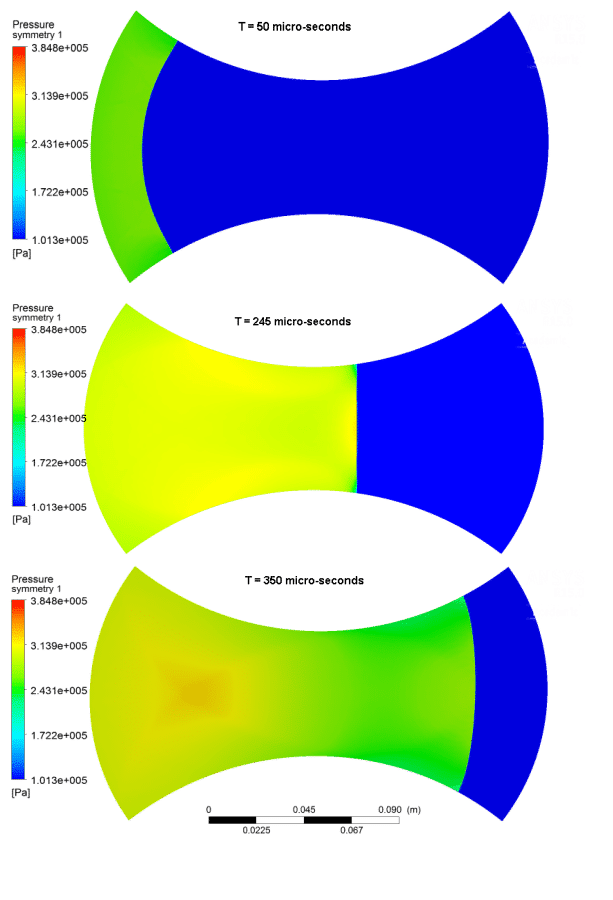
Figure 2: Preliminary CFD analysis of a curved shock (R = 465 mm) with a wall (R = 150 mm)
Comparison between CFD, numerical modelling and experiment will be achieved by comparing shock curvature, shock speed and the identification of any special flow features that are shown by each method.
References
Milton, B.E., 1975. Mach Reflection Using Ray-Shock Theory. AIAA, 13(11), pp.1531--1533.
Prasad, P. & Parker, D., 2009. A shock ray theory for propagation of a curved shock of arbitrary strength. Bangalore: Indian Institute of Science.
Skews, B., 1967. The perturbed region behind a diffracting shockwave. Journal of Fluid Mechanics, 29(4), pp.705-19.

