Since the first introduction of the weighted essentially non-oscillatory (WENO) scheme in Ref. [1], the efficient implementation in Ref. [2] made the algorithm applicable to realistic problems. Despite the success, some analytic outcomes of the scheme were still called in question. It were Henrick et al [3] who first pointed out that WENO5 failed to pertain the fifth order accuracy at the critical point where f’j=0. They further proposed the necessary and sufficient conditions for a scheme to obtain the order. In order to provide remedies for WENO5, Henrick et al [3] proposed a carefully designed mapping function, through which the difference between the nonlinear weight and its linear counterpart will usually have the order of Dx3. The corresponding scheme was called as WENO-M, and the improvement on resolution was shown through the comparison with WENO5.
However, Borges et al [5] argued the improvement was not due to the enhancement of the convergence order, but came from the more “assignment of larger weights to discontinuous stencils”. Still conforming to the accuracy requirement as in Ref. [3], they proposed a new IS by taking advantage of a term with regard to higher order derivatives. The corresponding scheme was called as WENO-Z and preliminary tests showed its slightly better performance than that of WENO-M [3, 4].
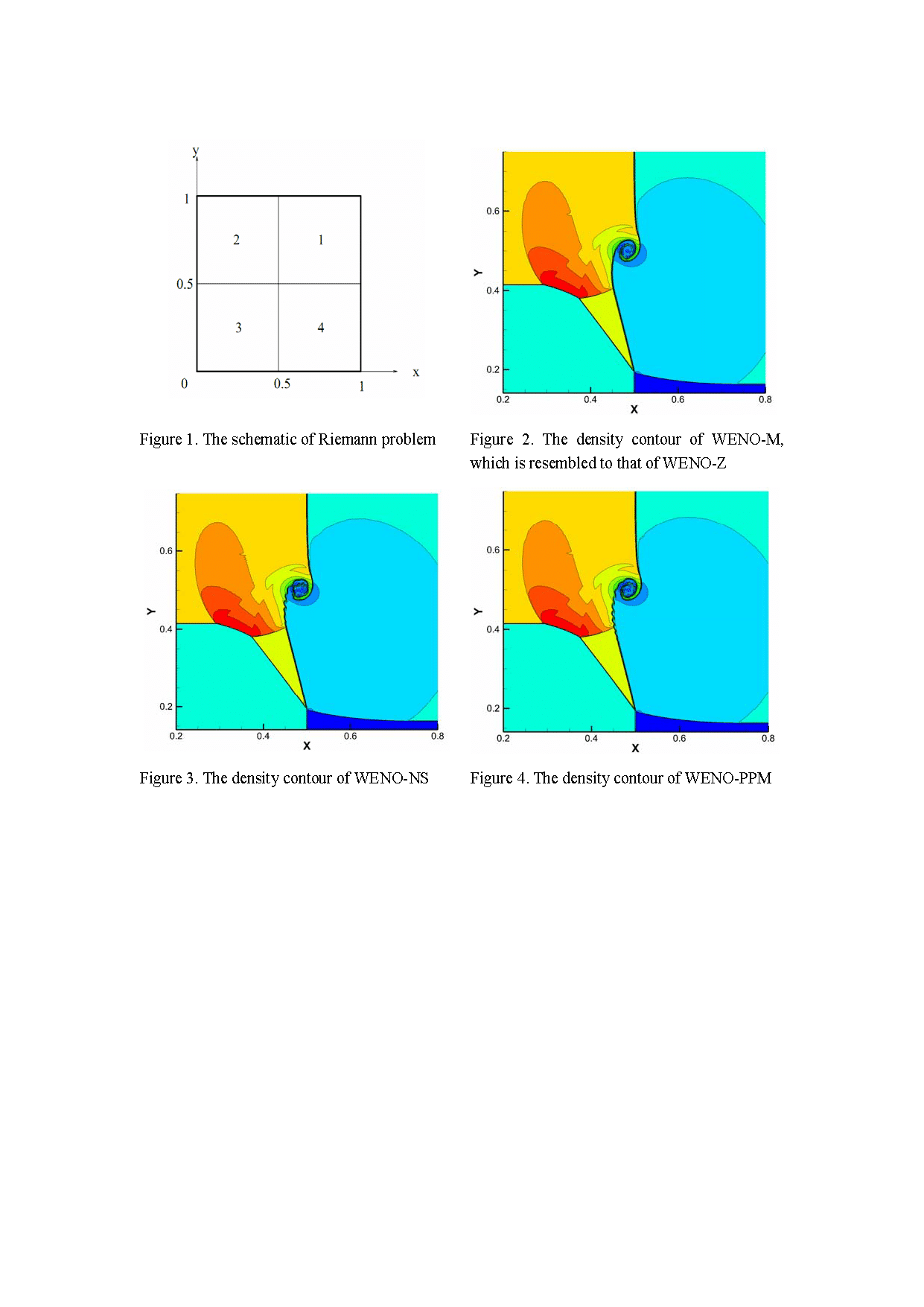
Still focusing on revising IS, Ha et al [4] proposed a new algorithm by combing numerical approximations of first and second order derivatives. The so-called WENO-NS scheme was proposed and the better capability of resolution was observed in the computations of double-Mach reflection and 2-D Riemann problems when compared with WENO-M and WENO-Z.
The enhancement of resolution sometimes has the potential risk of numerical instability. Our tests show that when using WENO-NS, the computation of a 2-D supersonic flow around half cylinder at M=4 will blow up, to say nothing of more tough hypersonic cases. So on the one hand, the high order and/or resolution are kept under pursuing, on the other hand the developed scheme is expected to be robust and have practical value.
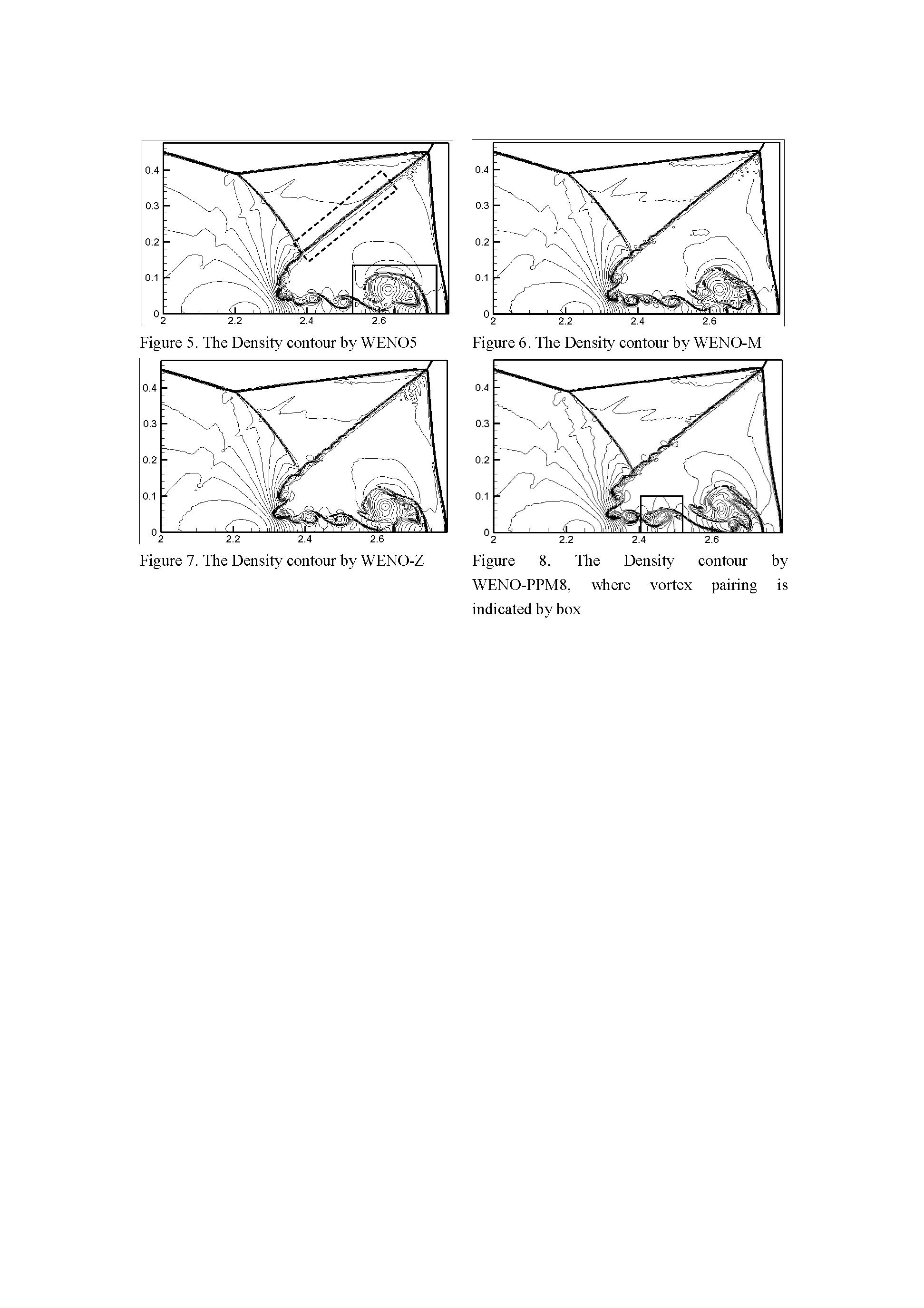
An attempt is tried in the paper for aforementioned purposes. Following the idea of mapping function, a new method is proposed, which is specifically designed for the resolution enhancement. Using the proposed methods, new fifth order WENO scheme is obtained and called as WENO-PPM. Typical numerical tests are conducted and compared with WENO5, WENO-M, WENO-Z and WENO-NS. According to the computation of the 2-D Riemann problem, WENO-PPM has processed the best performance; on the other hand the robustness of the scheme is indicated by hypersonic computations.
References
[1] X-D. Liu, S. Osher, T. Chan, Weighted essentially non-oscillatory schemes, J. Comput. Phys. 115 (1994) 200-212.
[2] S. Jiang, C.-W. Shu, Efficient implementation of weighted ENO schemes, J. Comput. Phys. 126 (1996) 202-228.
[3] K. Henrick, T. D. Aslam, J. M., Powers, Mapped weigted essentially non-oscillatory schemes: achieving optimal order near critical points, J. Comput. Phys. 207 (2005) 542-567.
[4] Ha, C.-H. Kim, Y.-J. Lee, J. Yoon, An improved weighted essentially non-oscillatory scheme with a new smoothness indicator, J. Comput. Phys. 232 (2013) 68-86.
[5] R. Borges, M. Carmona, B. Costa, W-S. Don, An improved weighted essentially non-oscillatory scheme for hyperbolilc conservation laws, J. Comput. Phys. 227 (2008) 3191-3211.