Methods based on shock-wave impact on the substance are used widely to create innovative materials throughout the world. The production of composite materials, in particular, materials that based on multi-component mixtures of metallic and non-metallic powders are of great interest. Shock-wave loading (SWL) of such mixtures can activate the chemical and phase transformations of the substances and contribute to the creation of entirely new materials with unique properties.
Efficiency of studies SWL of the multi-component mixtures with the aim of creating new materials depends on the possibility of predicting the behavior of the components based on the properties of each component in the mixture and its contribution to the process with different intensities of dynamic effects. It seems impossible construct of the model, which will describe all the factors associated with the given process, at present. Therefore the question of creating models that allows you to calculate at least the thermodynamic pressure, density, mass velocity and temperature for each component of the mixture comes to the fore. There are a lot of the models, but they all are adapted to the occasion with maximum of two condensed components in the mixture and they work in limited ranges of possible pressures. It should be noted the calculation methods based on the use of wide-range equations of state (EOS) of substances. With their help it is possible to calculate the parameters of the SWL of multi-component mixtures, but the EOS for each of the components of the mixture contain dozens of free parameters and experimentally determined constants. In this regard, the calculations become very cumbersome and time consuming.
In this work the thermodynamically equilibrium model TEC (thermodynamic equilibrium components) is proposed to describe the behavior of solid and porous materials and mixtures. The presence of gas in the pores taken into account in the model, as one of the components.. The model is based on single-speed and one-temperature approximation and at the same pressure for all phases. Equations of state of the Mie–Grüneisen type are used to describe the behavior of the condensed phases. For the gas, we use the equation of state of ideal gas. We write the conditions of dynamic compatibility on the shock wave front, which are laws of conservation of the mass flux for each component of the mixture and laws of conservation of momentum and energy fluxes for the mixture as a whole. The resultant equations combined with the EOS for each component are sufficient to find dependences, which can be treated as the shock adiabats (SA) of the multi-component mixture. We suppose that the Grüneisen coefficient depends explicitly only on temperature for condensed components, as the result, no more than five free parameters are used for each component.
Some of the results of the comparison calculations [1–3] for the TEC-Method with known experimental and calculated results of the different authors are listed below. The calculations for TEC-Method are shown In Fig. 1 for aluminum when the porosity values m from 1.4 to 8, where m is the ratio of the densities of the solid and porous substances. The calculated data correspond well to the data obtained on the basis of experiment.
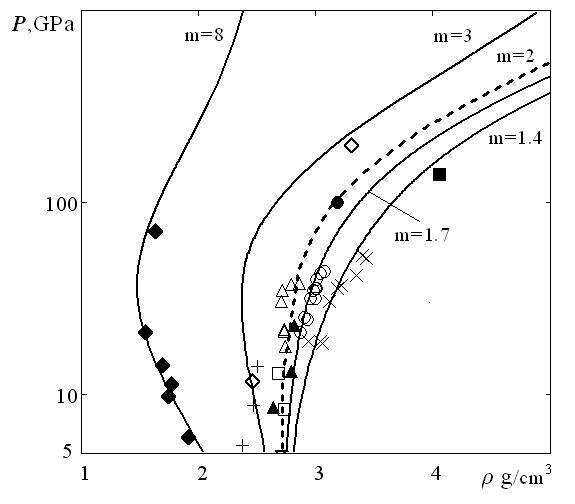
Fig.1. Diagram of porous aluminum.
The calculations of the mixtures with two solid phases on the TEC-Method shows that the model describes well the data of SWL of the mixtures with the components having similar parameters, and for the mixtures with significantly different parameters of the components. The calculations for the mixture of tungsten and paraffin that have the large difference values of density were given in [4] for the three models, with varying degrees of accuracy describing the data obtained on the basis of the experiment. The calculations are shown for the SC-Criterion (single component), the KEA-Method (kinetic energy averaging). These two methods operate on the principle of additivity, which is widely used, giving a satisfactory description of the experiments at relatively low pressures for alloys. The third model is the Turbulent Entropy Method; the attempt is made to consider the interaction of the components. Adding to the figure from [4] the curve calculated on the TEC-Method, it can be seen that only the model made it possible to adequately describe all the available data of SWL of the tungsten-paraffin mixture Fig. 2.
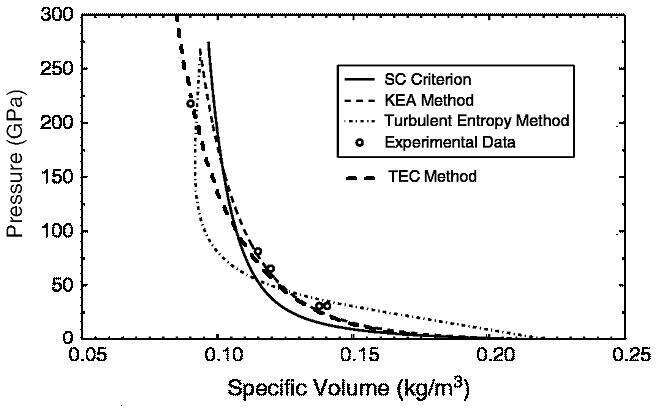
Fig. 2 Diagram of mixture tungsten-paraffin.
The TEC-Method allows you to describe including the region of the polymorphic phase transition, considering the investigated material in the region as the mixture of phases of low and high-pressure phases. The SA of the mixture with equal volume fractions of aluminum nitride AlN and silicon nitride Si3N4 is shown in Fig. 3, taking into account the phase transition in the nitrides.
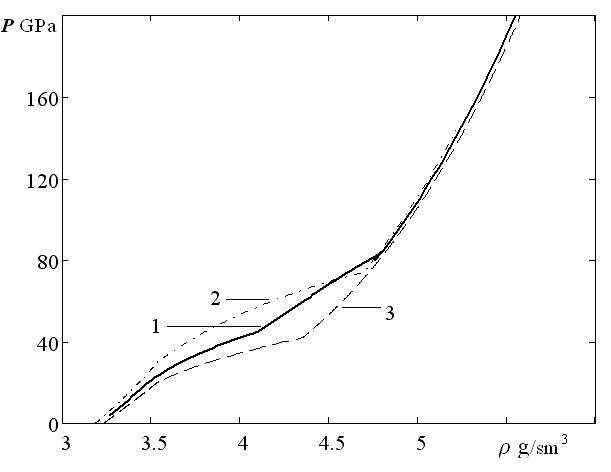
Fig. 3. Diagram of nitrides: 1 mixture Si3N4–AlN, 2 AlN, 3 Si3N4.
Thus, the presented TEC-Method allows to describe adequately the known results (SA, double compression shock waves, adiabatic expansion of shocked substance and temperature evaluation) in the whole range of possible pressures for virtually all solid and porous materials and mixtures for which experimental data are available. It should be noted that the proposed method of constructing the SA of the mixture allows you to monitor the compression not only of the mixture as whole, but also the compression of each component separately.
This work was supported by the Russian Foundation for Basic Research (project nos. 13-03-00663).
References:
- Kinelovskii S.A., Maevskii K.K. Comb. Explos. Shock Waves 2011.V. 47. Iss. 6. P. 706–714.
- Kinelovskii S.A., Maevskii K.K. J. Appl. Mech. Tech. Phys. 2013. V.54. Iss.4. P. 524–530.
- Kinelovskii S.A., Maevskii K.K. High Temperature. 2014. V. 6. DOI: 10.7868/S0040364414050081.
- Oren E. P., Francois X. J. Shock Waves. 2010 V. 20. P 73–83.

