In this paper we study shock ignition of reactive particles in a shock tube environment. When shock propagates through a cloud of reactive particles, the cloud is shifted, compressed, and the internal cloud temperature increased. In most experimental work a closed shock tube is used to allow the shock to reflect and propagate through the cloud a second time, further increasing the particle temperature. We use a multi-phase version of the numerical Regularized Smoothed Particle Hydrodynamics (RSPH) method, Omang and Trulsen (2014), to study shock ignition, and discuss important parameters that affect the particle ignition process. Although available experimental data on shock ignition of reactive particles are rather sparse, we compare our results to existing published experimental and numerical data. The agreement with published data is found to be acceptable.
In a multi-phase SPH each phase is described with a separate set of equations of motions, coupled through source terms. In the case of non-reactive particles, the two phases are coupled through heat and drag terms. In the case of particle ignition and combustion, radiation and mass exchange between the phases must also be taken into account. In the present work we use Ingebo drag coefficient (1956), the Knudsen and Katz (1958) Nusselt number, and the Chapman and Cowling (1961) dynamic viscosity. For aluminum particles the mass-burning rate suggested by Khasainov and Veyssiere (1987) is used. A dilute particle distribution is assumed in the current work, thus neglecting particle-particle collisions for the aluminum dust phase. A void fraction is introduced to describe the dust and gas distribution in the different problems, where the total sum should equal unity.
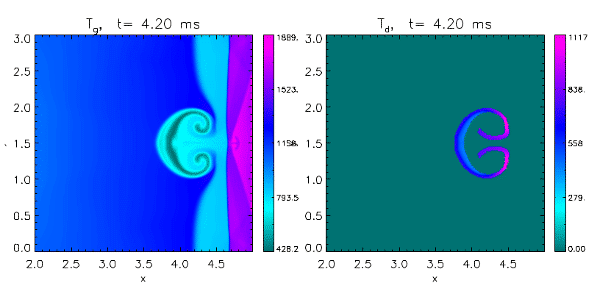
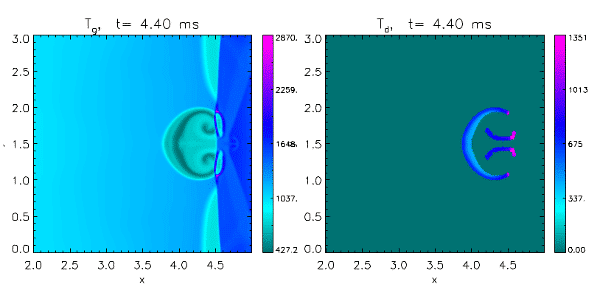
The number of experimental studies on shock ignition of aluminum particles published is rather sparse and often not fully documented. Here we have designed a representative test experiment, as illustrated in the Figure, where results from a 2D numerical simulation of a shock tube experiment are plotted. Initially, a closed-end 5 m long shock-tube, with a narrow driver section of 0.5 m is filled with high pressure and high density gas, generating a Mach 3.69 shock wave propagating from left to right. The propagating shock hits an initially circular-shaped aluminum dust cloud of radius 0.4 m located at x=1.5 m. The aluminum has an initial temperature of 293.15 K and a void fraction of 0.0005. The two left panels show the gas temperature at two different time frames, whereas the right panels give the corresponding aluminum dust temperature. The temperature scales reflect the maximum temperature for the each panel.
When the shock propagates through the aluminum dust cloud, the shock is retarded and curved whereas the aluminum cloud is heated, shifted and deformed. Due to the curving of the shock, a Mach reflection will form on the rear side of the cloud. Since the tube has a closed end, the shock is reflected, as illustrated in the figure for the time t = 4.2 ms. A significant inhomogeneous aluminum temperature increase is observed. At time t = 4.4 ms the reflected shock has propagated into the rear part of the aluminum cloud, leading to an additional increase in the temperature and the subsequent aluminum dust ignition. In the current simulations, a threshold ignition temperature of 1350K is assumed. The burning aluminum dust is transformed into gas phase, and the aluminum particles here disappear, as the particles burn out. The aluminum combustion leads to a significant local increase in gas temperature.
In the present study we investigate some of the important parameters in the process of shock ignition of aluminum dust clouds, looking closer at both mass exchange formulations, and the important parameters, such as Mach number, reflected gas temperature, and particle diameter. The results are compared to other published numerical, experimental and empirical results where available. The RSPH method is found to be a promising one for further studies.
REFERENCES
- M. G. Omang and J. K. Trulsen (2014), Multi-phase shock simulations with smoothed particle hydrodynamics. Implementation and applications to shock propagation through dusty gases. Shock Waves 24:521-536.
- Ingebo, RD. (1956), Drag coefficients for droplets and solid spheres in clouds accelerating in air streams. Technical Report TN 3762, NACA Technical Note TN
- Knudsen, J., Katz, D. (1958): Fluid Mechanics and Heat Transfer. McGraw-Hill, New York.
- Chapman, S., Cowling, T.G. (1961) The Mathematical Theory of Non-Uniform Gases. Cambridge University Press, Cambridge
- A. Khasainov and B. Veyssiere (1987), Analysis of the steady double-front detonation structure for detonable gas laden with aluminium particles. Archivum combustionis. Volume 7, number (3/4), pages (333-352).

