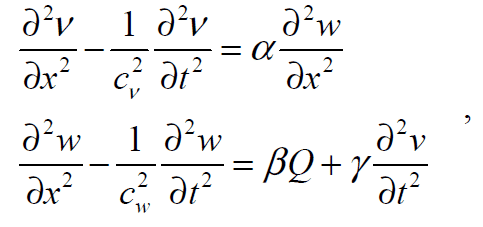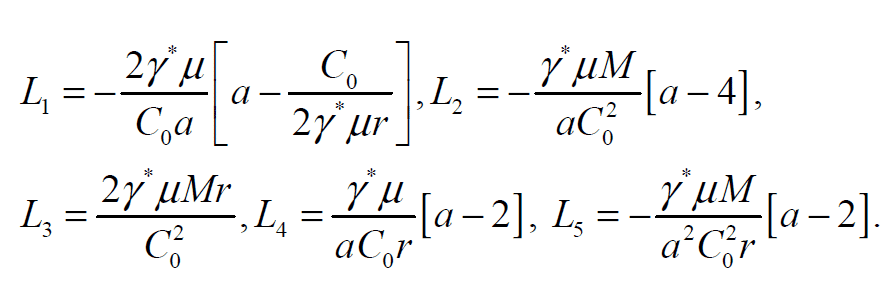MULTISCALE MODELING OF DYNAMIC DEFORMATION

In attempt to account for the multiscale mechanisms of straining, the first problem is how to describe a transition from one scale to another. Hard coupling between macroscopic and atom-dislocation dynamic variables doesn’t work. The sought transition must incorporate statistical variables which could provide a flexible linkage between scales. Also, there must be test regimes of dynamic deformation where theoretical approach could be experimentally verified. In this connection, one of the most convenient tests is known to be a steady-wave shock which is often used for verification of constitutive equations, determination of effective viscosity and developing the computation codes.

       In the present work, the propagation of steady wave in a medium with three levels of plastic deformation is considered: a) dislocation, b) meso-scale and c) macro-scale. To take into account the multiscale mechanisms of plasticity, an additional relaxation term describing the momentum exchange between meso- and macro scales is incorporated into a dislocation-based constitutive law. This item results from the particle velocity distribution at the mesoscale, so one can regard the motion of the shock front as a superposition of two modes: the mean motion of a plane front (mean particle velocity, u) and rapid fluctuations about the average value (particle velocity variance, D). In the case of dynamic processes, the elementary carries of deformation (ECD) (point and planar defects, dislocations, twins, etc.) cannot be identified. The only value which can be estimated by using interference technique is the space scale for correlated motion of ECD. From the point of view of mesomechanics, the correlated motion of ECD looks like pulsation of particle velocity characterized by the particle velocity variance D. The scale of meso-particle d_p, is estimated to lie within the interval _λ0<< d_p <<L, where_λ0 is the wavelength of laser radiation and L is diameter of the laser beam.

       In our approach, the additional deposit into total plastic deformation is incorporated in form of deformation variance, Δε. In one-dimensional case, analogously to the average plastic deformation, ε_av= u/C₀, the additional deformation caused by the variance of particle velocity can be written in the following form:

                                                               Δε = D/C₀.                                           (1)

     Experiments on shock loading of heterogeneous media reveal the existence of correlation between velocity variance and strain rate: the time-profiles of the particle velocity variance, D(t) and the strain rate, dε/dt change in parallel, so one can write

D = R dε/dt                      (2)

     For grounding the empirical relationship (2) we consider two-component model for heterogeneous material, which consists of two identical crystalline lattices connected with nonlinear interaction force the simplest form for which can be taken as follows

Q(w,dw/dt) = K sinlw+n dw/dt                     (3)

where K defines a maximum value of Q, coefficient n characterizes dissipation and λ determines a period in crystalline lattice. In essence, the function w (relative displacement) appears to be a latent degree of freedom, which may have a serious influence on dynamics of the system. Actually, it plays the same role as dispersion, that`s why dw/dt is considered to be analogue of the particle velocity variation D. Eq. (3) is supplemented with balance equations

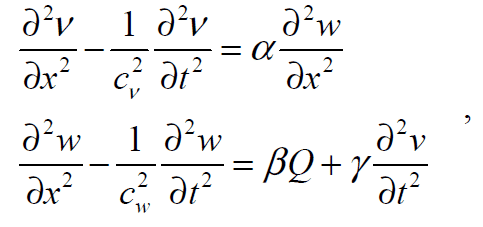(4)

where c_v²=(E₁+E₂)/(ρ₁+ρ₂) stands for the center of mass velocity and c_w²=E₁E₂(ρ₁+ρ₂)/(E₁+E₂)/(ρ₁ρ₂) signifies the velocity of relative displacement. Here E_i is Young`s modulus, ρ_i stands for the density of each component, v_i signifies the displacement (i = 1,2). The interaction force, Q depends on the properties of material. Specifically, it should take into account the possibility for undergoing phase transitions. Such method is rather well-known, but its usage in dynamic problems has not been studied properly yet [1].

Solution to Eqs. (3)-(4) results in relation between partial derivatives with respect to spatial coordinate and time

dw/dx=–1/C₀ dw/dt                            (5)

which is analogous to expression (2).

   We apply Eqs. (1) - (2) to form the additional relaxation term in constitutive equation of Taylor-Duvall [2]:

σ_t – ρC_l²ε_t=–2μ(ε_t^d+R/C₀ε_tt)             (6)

The right part of this equation consists of two terms. The first one Δε_t^d describes the contribution of dislocations into the total strain rate. The second term presents a collective mechanism, stipulated by the particle velocity variance. Balance equations

ρu_t+σ_x=0     (7)

u_x+ε_t=0       (8)

and constitutive equation (6) yield the closed set of equations describing the propagation of steady plastic wavefront in heterogeneous medium with mesoscopic effects taken into account. Introducing one independent variable z = x–C₀t leads to the following equation with respect to the particle velocity u:

u_zz+L₁u_z+L₂uu_z+L₃u_z²+L₄u+L₅u²=0,         (9)

where

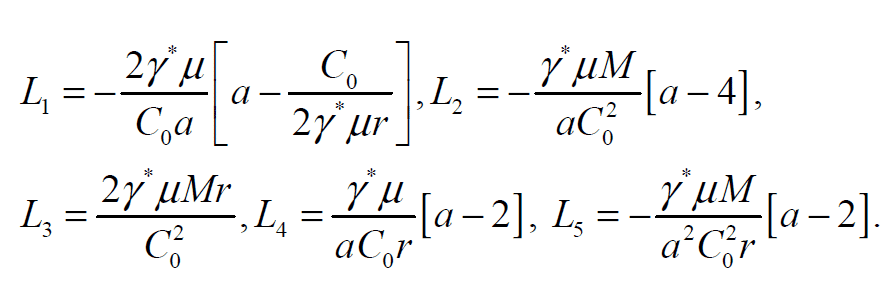
Eq. (9) is the second order non-linear differential equation describing a steady plastic front. The problem of approximation of a profile and determining parameters of models is complicated by presence both useful and spurious components in experimental data, which are represented by additive and multiplicative noise. In order to denoise signal the algorithms of wavelet-filtration have been used [3]. To solve the problem of estimating the coefficients the Levenberg - Marquardt algorithm [4] based on heuristics have been used. The optimization algorithm completed when the root-mean-square deviation between estimates and the experimental data does not exceed the established threshold for accuracy. Free surface velocity profile U_fs, calculated by using the suggested model is presented in Fig. 1.

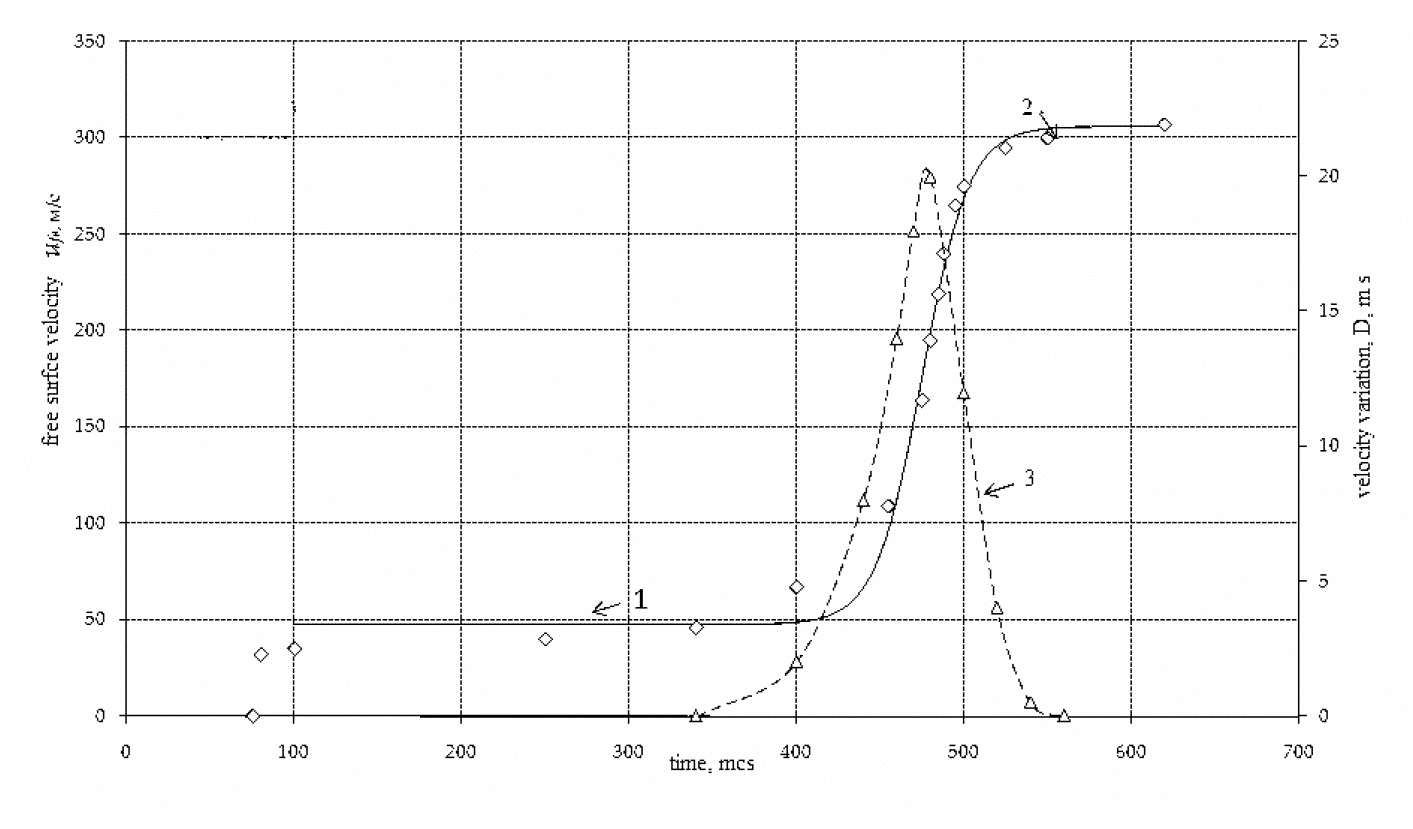
Fig.1. Experimental data for free surface profile (1), calculated free surface profile (2), velocity variation profile (3) obtained for aluminum alloy D16 target loaded at the impact velocity of 315 m/s.

References

1. Indeitsev D. A., Naumov V. N., Semenov B. N. Dynamic effects in materials of complex structure. (2007). Mechanics of Solids. Vol. 42. No. 5, 672-691.
2. Taylor J.W. Dislocation dynamics and dynamic yielding. (1965). J. Appl. Phys.Vol. 36, No 10, 3146-3155.
3. Mallat S. Wavelet Tour of Signal Processing. (1998) Second Edition. Wavelet Analysis &Its Application, Academic: New York.
4. Gill P.E., Murray W., Wright M.A. Practical Optimization. (1982 ) Academic Press, New York.