The study of shock wave attenuation has drawn much attention in shock wave community. One of the common ways to attenuate shock waves is to arrange multiple obstacles to block the propagation path of the shock wave [5]. We propose an arrangement of the obstacles by placing the square or cylinder shaped obstacles along the outline of a logarithmic spiral curve [3] (Figure 1), taking advantage of its ability of collecting the incident shock wave with specific Mach number [4] to its focal region [1, 2]. We simulated the process of the shock wave passing through these arrangements using the Euler equations of gas dynamics. Then, to validate the numerical results, we present corresponding experiments under the same initial conditions. Results show that the numerical and experimental methods agree well, and that placing obstacles along a logarithmic spiral curve can effectively attenuate the transmitted shock waves.
In the simulation part, Overture, a framework to solve partial differential equations using finite differences on overlapping grids is used. Information regarding the solver and its packages can be found at http://www.overtureframework.org/. In this research, we employ the Composite Grid Compressible Navier-Stokes (CGCNS) solver that can be used for solving either the compressible Navier-Stokes or the inviscid Euler equations. All the work presented here is governed by the two-dimensional inviscid Euler equations and a second-order Godunov scheme is used for these cases. AMR is used to accelerate the simulation process.
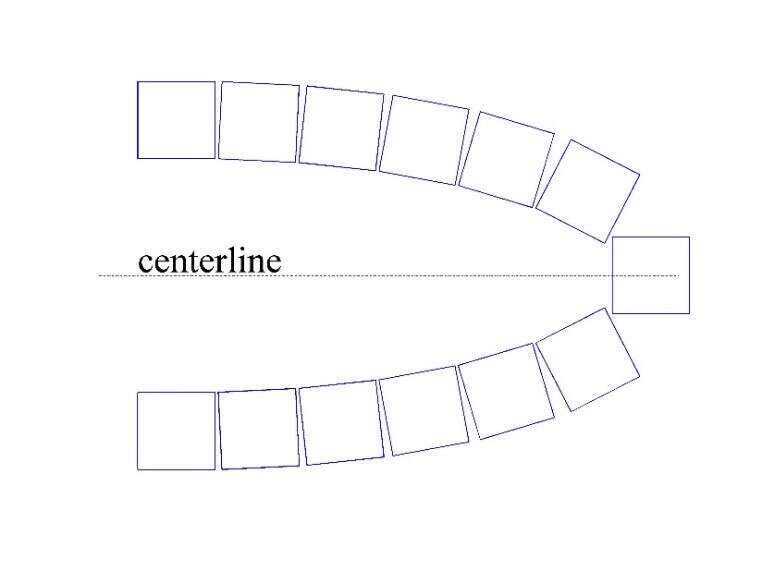

Figure 1. The placement of square and cylindrical obstacles along the outline of logarithmic spiral curve
In the experiment we used aluminum to build the square and cylinder shaped obstacles. Two pressure sensors, one upstream and the other downstream of the obstacle configuration, are used to measure the pressure change through time. A high-speed camera is used to capture a video of the shock wave during the whole process using the schlieren imaging technique.
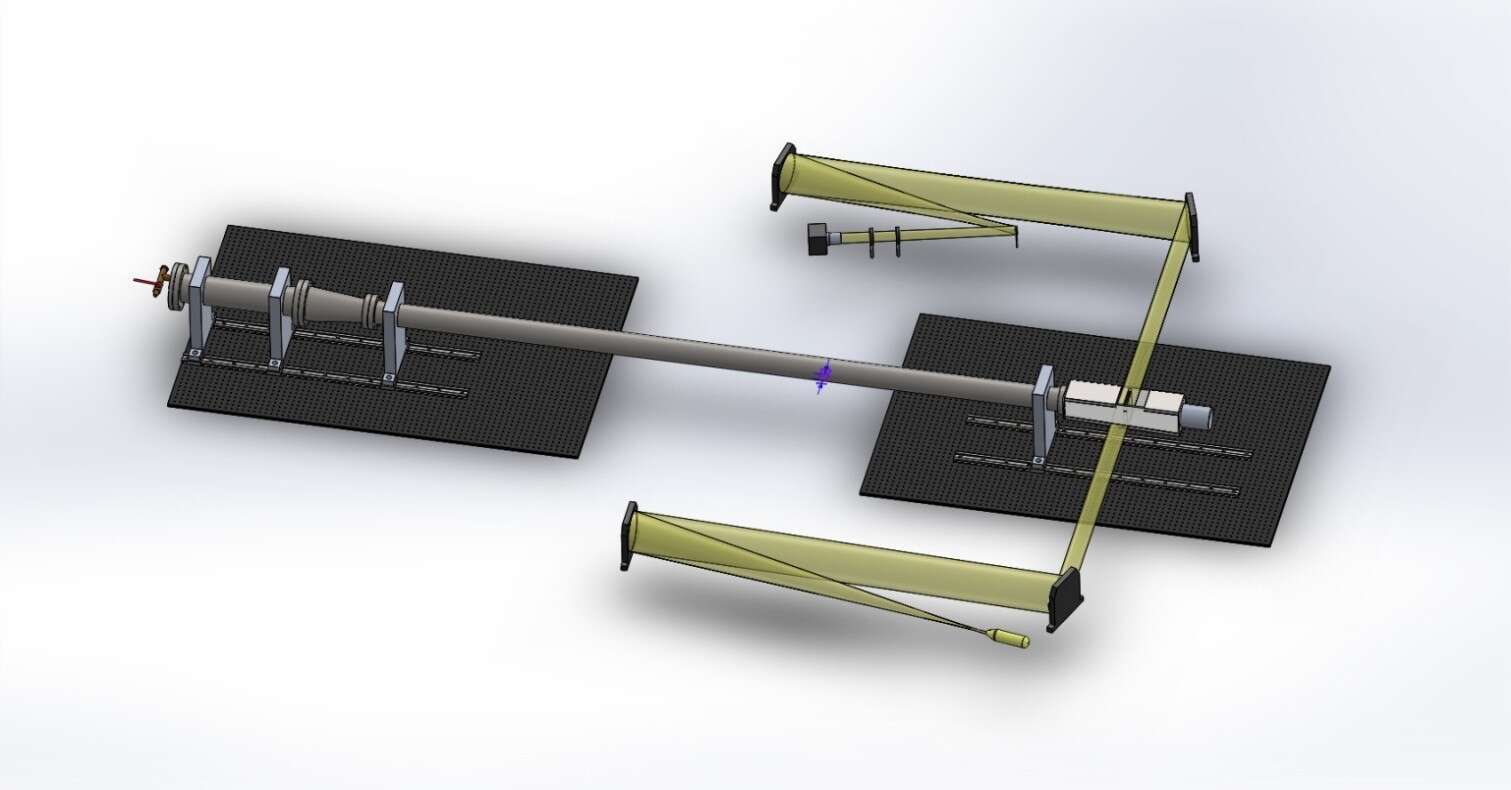
Figure 2. Experimental setup
The simulation and experimental setup is shown in Figure 3. The size of the test section is 711.2 × 50.8 mm. The distance between the left end of the shock tube and the initial location of the shock wave is 283.2 mm (x = −20 mm), while the leading edge of the obstacles is set at x = 0. Two probes are located in the test section to record the pressure change through time. One is set at x=-105.4 mm, which is 177.6 mm to the left boundary. The other probe is put at x=319.53 mm, which is 108.67 mm to the right boundary. A two-dimensional duct flow scenario is considered, where obstacles are placed in varying geometric configurations to attenuate a normal shock wave impacting the obstacle configuration from the left. The top and bottom walls of the duct are parallel to each other, simulating part of the test section.

Figure 3. Simulation and experimental setup. A two-dimensional test section where planar shock wave impacts on the obstacles from left to right. Distances in mm. Not to scale.
Figure 4 shows a comparison of the schlieren images of the first test for both the simulation and the experiment.
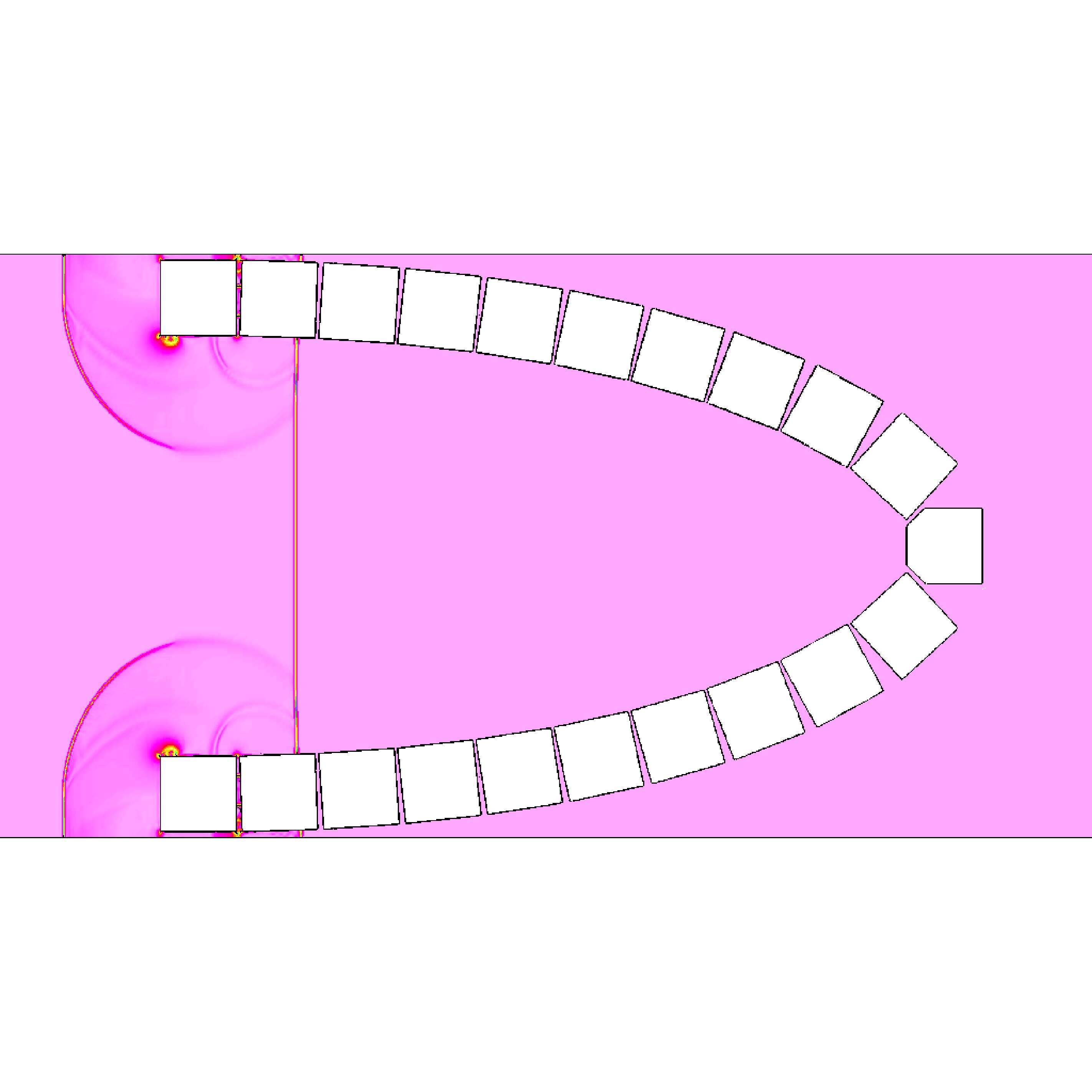
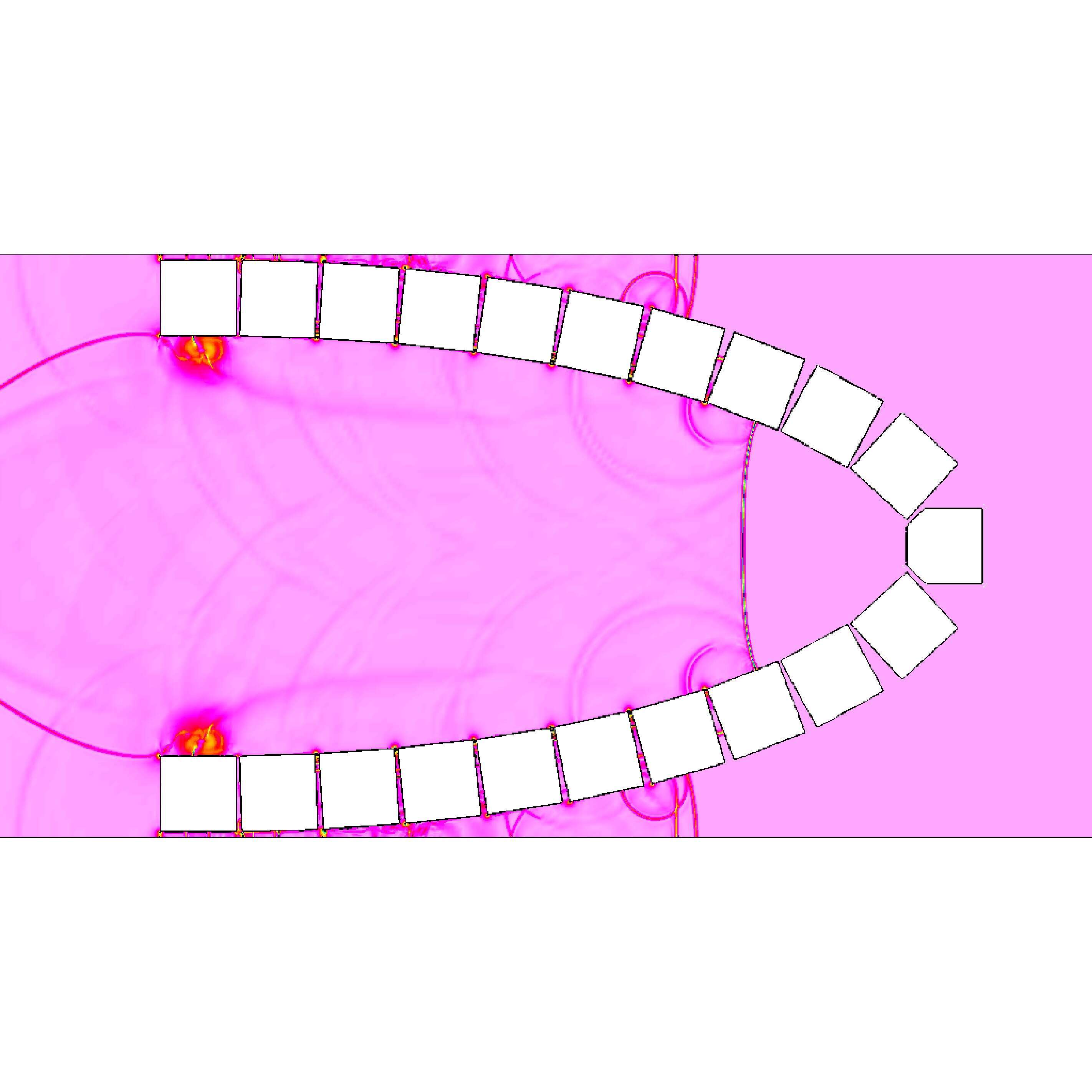




Figure 4. Schlieren images for simulation and experiment at the same instant time
A future direction of this research will be to investigate the same scenario using different shapes and materials of obstacle that can help to further attenuate the shock wave. By choosing materials wisely, larger shock attenuation should be possible.
References
[1] Inoue, O., Imuta, S., Milton, B., Takayama, K. (1995) Computational study of shock wave focusing in a log-spiral duct. Shock Waves 5, 183–188
[2] Inoue, O., Takahashi, N., Takayama, K. (1993) Shock wave focusing in a log-spiral duct. AIAA J 31(6), 1150–1152
[3] Milton, B., Archer, R. (1969) Generation of implosions by area change in a shock tube. AIAA J 7(4), 779–780
[4] Whitham, G. (1974) Linear and nonlinear waves. Wiley-Interscience, New York
[5] Chaudhuri, A., Hadjadj, A., Sadot, O., Ben-Dor, G. (2013) Numerical study of shock-wave mitigation through matrices of solid obstacles. Shock Waves 23, 91–101

