Interaction of oblique shock waves arising in a supersonic steady two-dimensional monatomic gas flow about two symmetrically located wedges is considered. Two different (regular and Mach) shock wave configurations can be formed in such flows [1, 2]. The case of regular reflection is analyzed in the present work.
An exact solution in the vicinity of the reflection point is known for the inviscid gas model. This solution consists of three zones with constant parameters, which are separated by two infinitely thin discontinuity lines: incident and reflected shock waves. In the case of a viscous gas, these shock waves have a finite thickness, and a viscous flow region with a size of approximately ten mean free paths is observed in the reflection point; moreover, there is a wake with a length of about one hundred mean free paths downstream of this region [3]. It should be noted that this problem in a certain sense is an extension of the classical problem of the kinetic theory of gases about the structure of a plane shock wave. However, the present problem is more complicated due to two-dimensional effects. As in the problem of the shock wave structure, viscosity plays a key role in the present problem. At high Mach numbers, effects of rarefaction and thermal nonequilibrium may also be important. The goal of this work is a numerical analysis of the influence of the above-mentioned effects on the flow near the reflection point by means of comparisons of results simulated with the use of different mathematical models: Navier-Stokes equations, moment equations (R13), and Boltzmann equation (both the direct numerical solution and the Direct Simulation Monte Carlo (DSMC) computations).
Some results of numerical simulations for an argon flow with the free-stream Mach number equal to 20 (Mach number normal to the incident shock wave equals 8) are presented below. Figure 1 shows the temperature field computed by the DSMC method and by solving the Navier-Stokes (NS) equations. The coordinate is normalized to the mean free path in the incoming flow. It is seen that the DSMC method predicts an appreciably greater thicknesses of the incident and reflected waves than the NS equations owing to the thermal nonequilibrium effects taken into account in the DSMC computations. The temperature field in the DSMC solution has a clearly expressed temperature peak in the wake behind the reflection point.
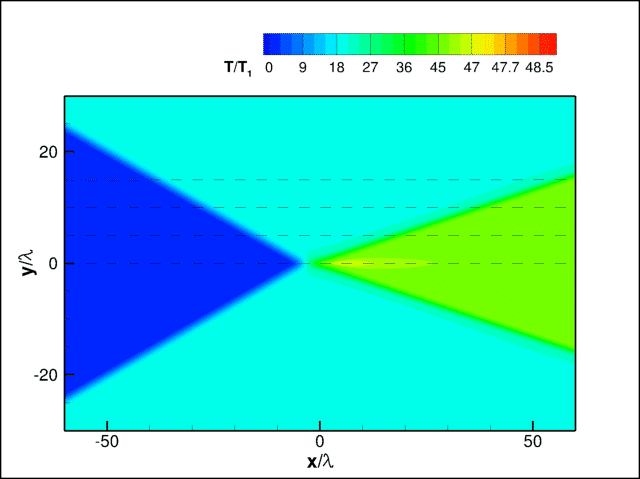
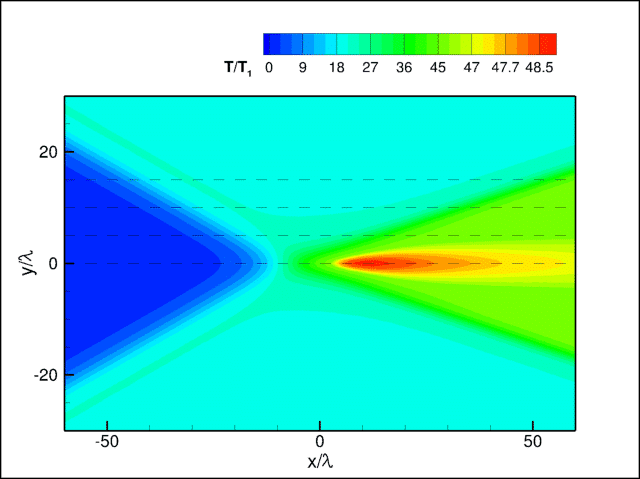
Fig. 1. Temperature fields. NS (upper plot) and DSMC (lower plot).
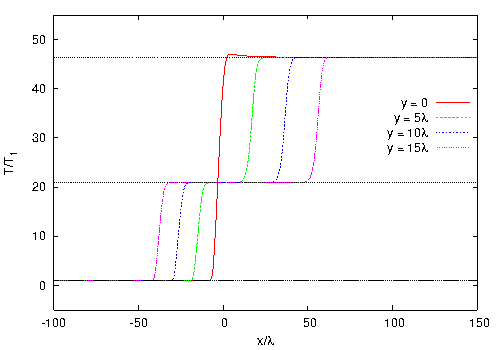
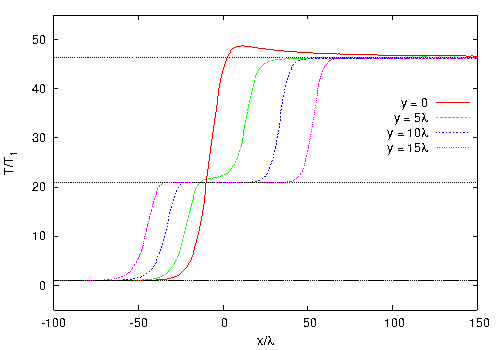
Fig. 2. Temperature profiles. NS (upper plot) and DSMC (lower plot).
Figure 2 shows the temperature profiles calculated by the DSMC and NS methods along the horizontal lines y = {0, 5λ, 10λ, 15λ} shown by the dashed lines in Fig. 1. The horizontal dotted lines show the theoretical values of macroparameters derived from the Rankine-Hugoniot relations. It is seen that the temperature in the DSMC results reaches a constant value (behind the reflected wave front) along the plane of symmetry at a distance of about 150λ from the origin of the coordinate system, while the constant temperature in the NS simulations is reached much faster (about 25λ). However, at a certain distance from the straight line y = 0, long-time equalization of temperature is not observed. In this case, there is an intermediate value on the profiles (corresponding to the zone behind the incident wave front). A significant difference between the shock transition thicknesses in the DSMC and NS simulations should also be noted. In the plane of symmetry, the temperature profile predicted by the DSMC method has a considerable peak whose magnitude (relative to the value behind the reflected wave front) is several-fold higher than the corresponding value in the NS computations.
The full paper will present results demonstrating that there is a zone of a strongly nonequilibrium flow in the vicinity of the reflection point, which is not described by the continuum approach. Thermal nonequilibrium of the flow in the vicinity of the reflection point will be analyzed both in terms of different temperature components and in terms of the molecule velocity distribution function.
References
[1] Ben–Dor, G., “Oblique Shock Wave Reflections,” Handbook of Shock Waves, edited by G. Ben-Dor, O. Igra, and E. Elperin, Academic Press, New York, Vol. 2, 2001, Chap. 8.
[2] Hornung, H., “Regular and Mach Reflection of Shock Waves,” Annual Review of Fluid Mechanics, Vol. 18, No. 1, 1986.
[3] D. Khotyanovsky, Y. Bondar, A. Kudryavtsev, G. Shoev, and M. Ivanov,“Viscous effects in steady reflection of strong shock waves,” AIAA Journal 47, 1263–1269 (2009).

