Application of mathematical programming for analysis of experimental data obtained at the Hopkinson’s stand

One of the most common methods for studying the behavior of materials in the speed range deformation 10²-10⁴ is the use of the split Hopkinson-Kolsky bar [1,2]. There are various methods through calibration of such experimental stands [3], however, these methods do not resolve a number of factors: the variance of forms of the loading pulse, inaccuracies timing pulses and the presence of noise components, etc., which influeces on the methods of determining properties of materials, such as incubation time [4]. Therefore, it is necessary to use digital signal processing techniques for filtering and analysis of experimental data as an interconnected triad of the loading, the reflected and transmitted pulses.

An effective algorithm for collaborative filtering and joint analysis of experimental signals received at the Hopkinson’s stand has been found. It is shown that this problem can be formulated as a mathematical programming problem, and it is reduced to quadratic programming when interconnected triad of the loading, the reflected and transmitted pulses are filtered, and it is described as a sequence of quadratic programming problems in the case when the pulses are filtered and the phase shifts between them had been calculated as well.

The proposed filtering and analysis algorithms were used to identify components of the signals [5], which are due to the influence of the experimental stand and eliminate them with further calculation of properties of materials, resulting in a significant (»2 times) reduction in MSE. In contrast to standard filtering techniques (Fourier transform, wavelet analysis, correlation analysis) in the proposed algorithms comes from relations that do not contradict to the physics of the tested material . These algorithms can be improved by the introduction of new rheological models of materials.

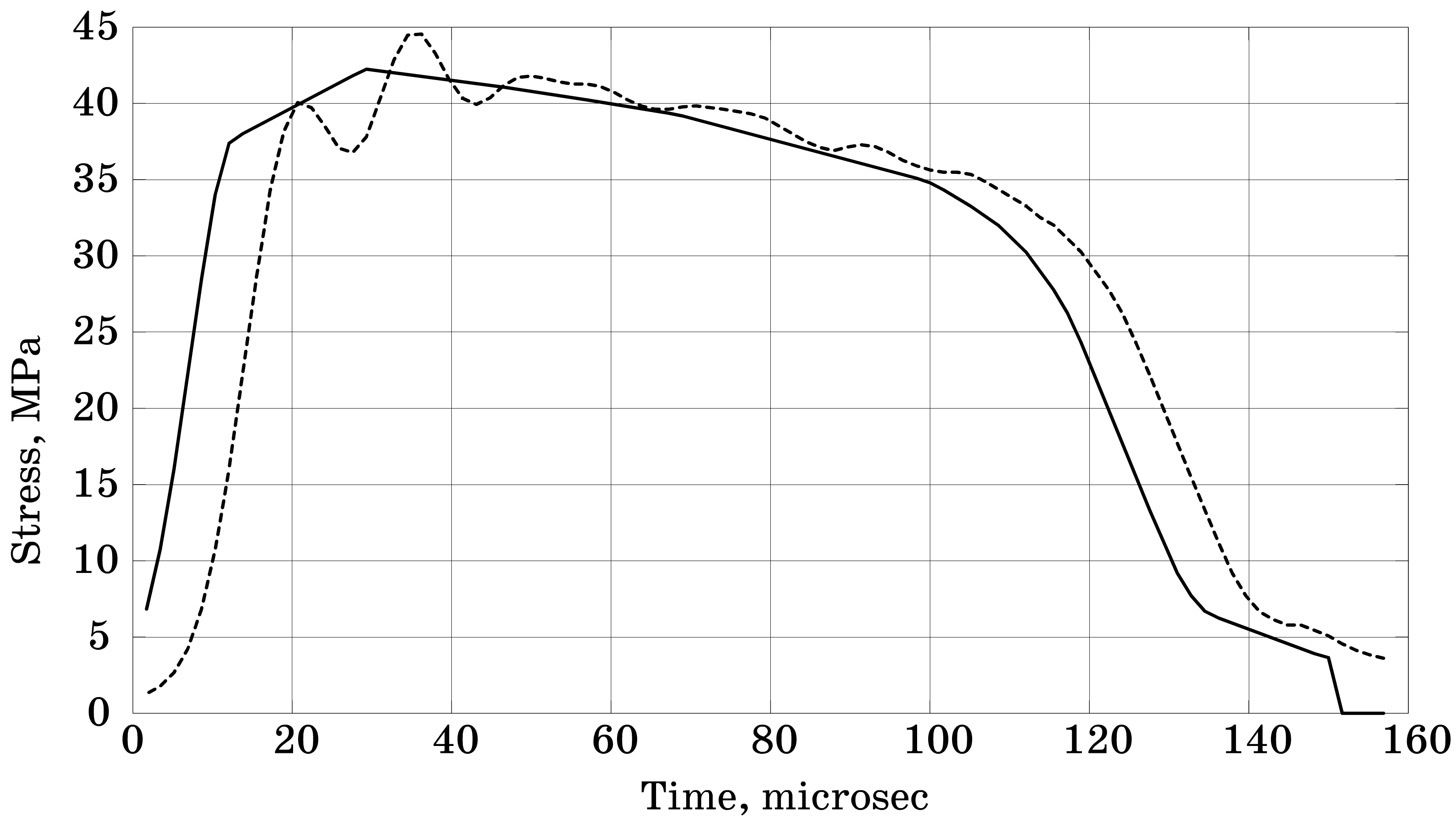
Figure 1 shows the results of filtering experimental signals measured on the transmitted bar. The dashed line specifies initial data and the solid line specifies filtered data.

The researches were conducted under the grant RFBR №13-01-00349.

Keywords – split Hopkinson-Kolsky bar, mathematical programming, digital signal processing.

References

1. Hopkinson B. A Method of Measuring the Pressure Produced in the Detonation of High Explosives or by the Impact of Bullets // Philos. Trans. R. Soc. (London) A, 1914, 213, 437-456.
2. Kolsky H. An investigation of mechanical properties of materials at very high rates of loading // Proceedings of the Physics Society of London. – B62. – 1949. – P. 676-700.
3. Nikolaeva E. A. Osobennosti dinamicheskoi kalibrovki sterzhnia Gopkinsona – Kol`skogo // Matematicheskoe modelirovanie sistem i protsessov, 2003. vol. 11, pp. 87-93, (In Russian).
4. Petrov Y.V. Incubation time criterion and the pulsed strength of continua: fracture, cavitation, and electrical breakdown // Doklady Physics, 2004, 49, 246-249.
5. Smirnov I., Petrov Y., Volkov G., Abramian A., Verichev S., Bragov A., Konstantinov A., Lamzin D. Dynamic Strength of Limestone in Terms of the Incubation Fracture Time Criterion. Procedia Materials Science, Vol. 3, 2014, Pages 778–783, 20th European Conference on Fracture.