The interaction of a propagating shockwave with a density interface is a fluid flow phenomenon of considerable interest due to its occurrence in
several natural phenomena and important technological applications. One of the classical shockwave-density interface interaction problems is that of a planar shockwave interacting with a cylindrical gas inhomogeneity (Haas and Sturtevant, 1987). The evolution of the interaction is dominated by vorticity, with a baroclinic source provided by the density gradient across the interface and the pressure gradient associated with the shockwave. The primary governing non-dimensional parameters for this problem are the Mach number and the Atwood number. This problem has been studied extensively in the past, both numerically and experimentally to understand effects of these parameters on evolution of the shock-bubble interaction (Quirk and Karni, 1996), (Ranjan, Oakley and Bonazza, 2011), although a comprehensive investigation covering a large range of these two parameters is still lacking.
In the present work, two-dimensional numerical simulations of the interaction of a plane shockwave with a cylindrical gas inhomogeneity are performed. The Euler equations of gas dynamics are used as the basic flow model in view of the fact that the viscosity effects are negligible for most of the time of interest. A finite volume reconstruction-evolution methodology is used for the simulations. High-resolution multi-fluid solvers are developed, using a fifth order weighted essentially non-oscillatory approach for spatial reconstruction and a third order Runge-Kutta scheme for temporal integration (Shu, 1997). Two inter-cell face flux evaluation schemes, comprising of approximate Riemann solvers available in the literature are incorporated (\cite{abstractRef6}). Multi-fluid simulation capability is achieved using the Ghost Fluid Method (GFM) that uses a level set approach for identification of the interface between the two fluids (Fedkiw et al. 1999). A thorough benchmarking of the solvers is performed using experimental and numerical simulation results available in the literature. Following the benchmarking of the codes, a parametric study for a wide range of the Atwood number, ranging from -0.7 to 0.7, and for a shock of Mach 1.22 is performed. The results of the parametric study are presented qualitatively using schlieren images of the developing flow field, and quantitatively by providing time-sequence data of the evolution of the integral features of the gas bubble such as axial and lateral dimensions, translational velocity of the bubble, circulation in the flow-field and of stretching rates experienced by the bubble. Figures 1 and 2 depict results for the axial deformation and the circulation in the flow-field. The behavior of these integral features is found to be consistent with the vorticity characteristics, which in turn, are determined by the baroclinic source term for the vorticity. The translational velocities and the maximum circulation within the flow-field are found to compare fairly well with analytical models available in the literature.
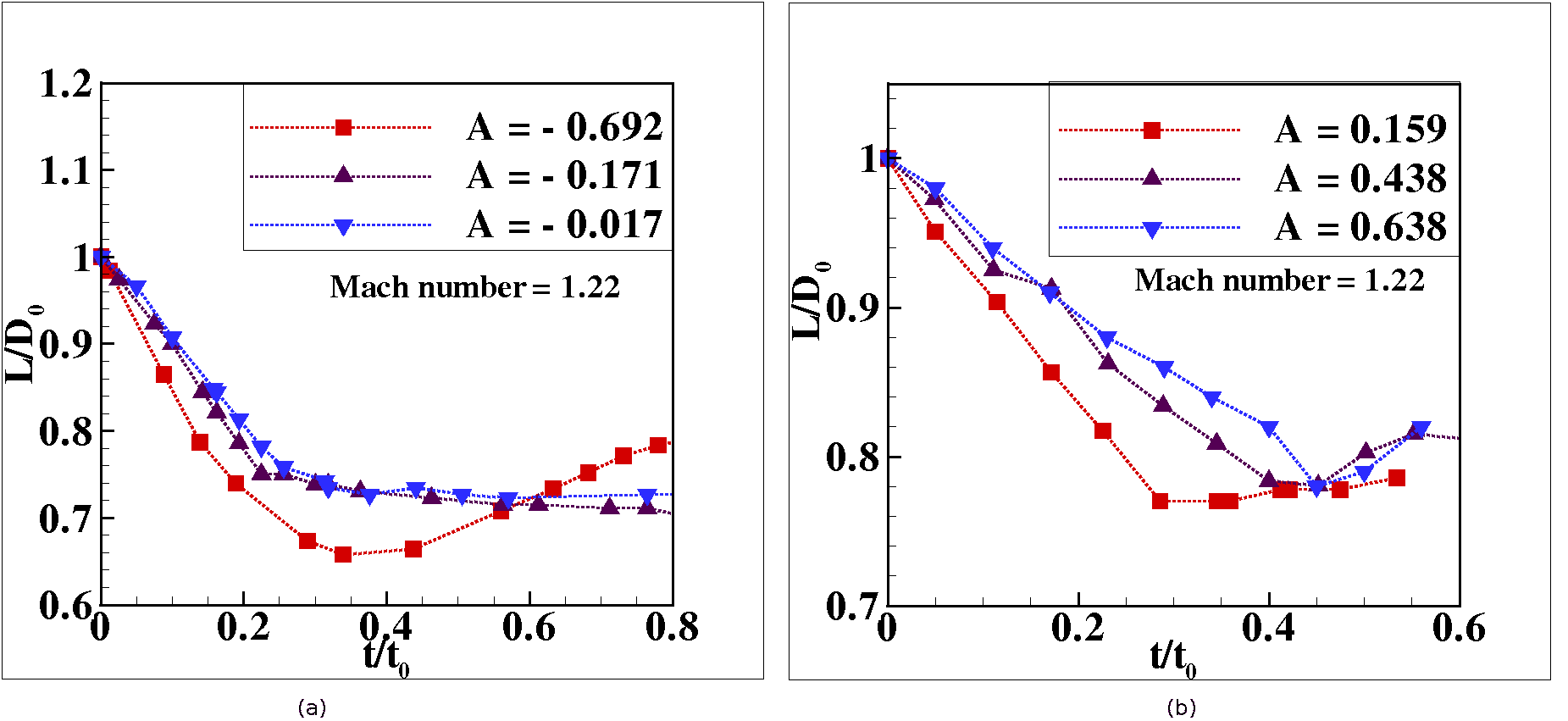
Fig. 1 Axial deformation behavior of a bubble at Mach 1.22. (a) Divergent cases, (b) Convergent cases.
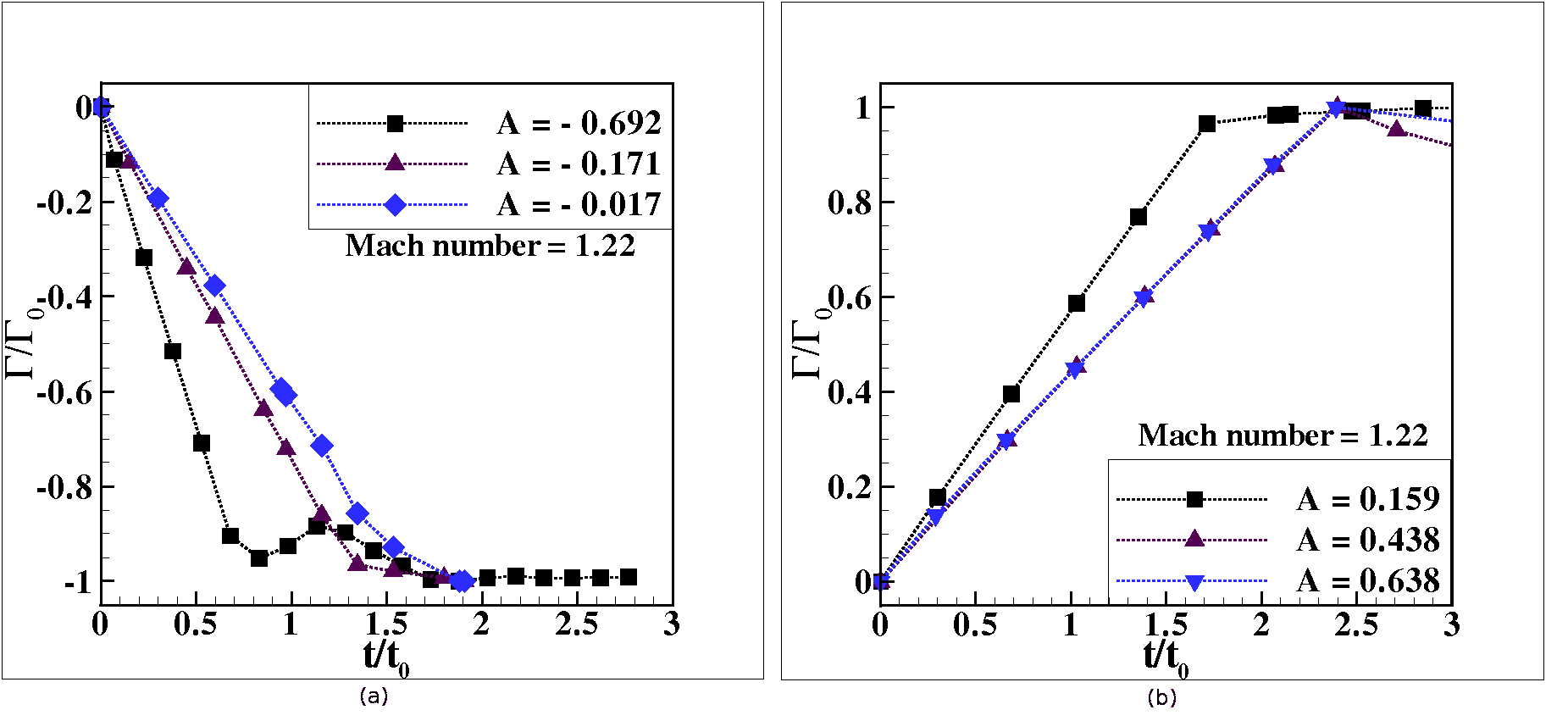
Fig. 2 Normalized circulation as a function of non-dimensional time at Mach 1.22. (a) Divergent cases, (b) Convergent cases.
References:
Haas J. -F., and Sturtevant B. (1987) Interaction of weak shock waves with cylindrical and spherical gas inhomogenities. J of Fluid Mechanics Vol. 181, 41-76
Quirk J. J., and Karni S. (1996) On dynamics of a shock-bubble interaction. J of Fluid Mechanics Vol.318, 128-163
Ranjan D., and Oakley J., and Bonazza R. (2011) Shock-bubble interactions. Annual Review Fluid Mechanics Vol.43, 117-140
Shu C.-W. (1997) Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. ICASE-1997-65
Fedkiw R.P., and Aslam T., and Merriman B., and Osher S. (1999) A non-oscillatory Eulerian approach to interfaces in multi-material flows (the ghost fluid method). J of Computational Physics Vol. 152, 457-492.
Toro E. F. Riemann solvers and numerical methods for fluid dynamics : A Practical Approach, Springer Verlag, Berlin, 1992

