It is well known that molecules of the flow behind a strong shock become vibrationally excited and the flow is far from thermal equilibrium. It is necessary to distinguish at least two temperatures: translational and vibrational. In near-continuum and rarefied flows, the zone of vibrational thermal relaxation is comparable with the characteristic length of the flow problem. This thermal non-equilibrium effect itself changes not only the flow structure; it also affects the dissociation rate. The chemical reaction rate, in particular, the dissociation rate, depends on both translational and vibrational temperatures. The difference between one-temperature and two-temperature reaction rate constants can be more than several times; it can lead to significant changes in the flow pattern. Therefore, an appropriate physical model is required to describe the chemical reaction rate in a non-equilibrium flow. Accurate modeling of the non-equilibrium flow is especially important, for example, for hypersonic aerothermodynamics of re-entry space vehicles.
The Fluent-neq code for the commercial Ansys Fluent flow solver is used for numerical simulation of flows with thermochemical non-equilibrium. The conservation equation of translational energy is solved separately from the equation of vibrational energy, which is added to the system of Navier—Stokes equations (conservation of mass, momentum, and translational energy). The translational and rotational modes are assumed to be in equilibrium, so only two temperatures (translational and vibrational) are distinguished. The Landau–Teller model is used for vibrational thermal relaxation. The vibrational relaxation time is calculated with the use of the semi-empirical formula by Millikan and White [1] coupled with the Park correction [2] for high temperatures. The density-based solver, specially developed for high-speed compressible flows, is used in a steady implicit formulation with an AUSM flux type and a second-order upwind scheme for spatial discretization.
In order to test the code used in this work, vibrational relaxation of nitrogen (N2) under adiabatic conditions was calculated and compared with available numerical results [3]. Figure 1 shows the time history of the relaxation process. At the zero time instant, the translational temperature T0 was set to 5000 K (left figure) and 20000 K (right figure), and the vibrational temperature was Tv0=200 K for both test cases. The solid curves "T" and "Tv" show the numerical solutions [3] of the Landau-Teller equation, which are in excellent agreement with DSMC computations [3]. The square symbols "T Fluent-neq" and "Tv Fluent-neq" show the results of the code being developed in this work. The numerical data obtained in the present work are in good agreement with the numerical data of [3] (see Fig. 1).


Fig. 1. Vibrational relaxation of N2 for T0=5000 K (left) and T0=20000 K (right), Tv0=200 K for both test cases.
A supersonic flow of the nitrogen mixture N2-N around a two-dimensional wedge (w=5.1 cm, the angle is 53.5 deg) is considered in this work. Freestream conditions correspond to experiments carried out in [4]: The Mach number is 7.7, the pressure is 940.3 Pa, the temperature is 1100 K, and the composition is 31.9 mol/kg for N2 and 7.7 mol/kg for N. Note that the Reynolds number and the Knudsen number based on freestream parameters are 14485 and 0.000652, respectively; therefore, the continuum approach can be used to simulate this flow. A supersonic inflow with the freestream flow parameters was set on the left boundary of the computational domain. The right boundary was located far enough downstream to provide the supersonic outflow condition. The symmetry condition was used at the lower boundary of the domain. The no-slip boundary condition was set on the wall of the wedge.
The temperature flowfields for the non-reacting and reacting cases are compared with the CFD-FASTRAN numerical solution obtained in [5] (see Fig. 2). In the case of the reacting flow, the Arrhenius rate constant, which depends only on the translational temperature, is used in both simulations, and two reactions of dissociation are taken into account (1. N2+N2→2N+N2; 2. N2+N→3N). It is clearly seen that both numerical solutions agree well with each other. Due to chemical reactions, the temperature behind the shock wave becomes lower and the stand-off distance of the shock decreases.
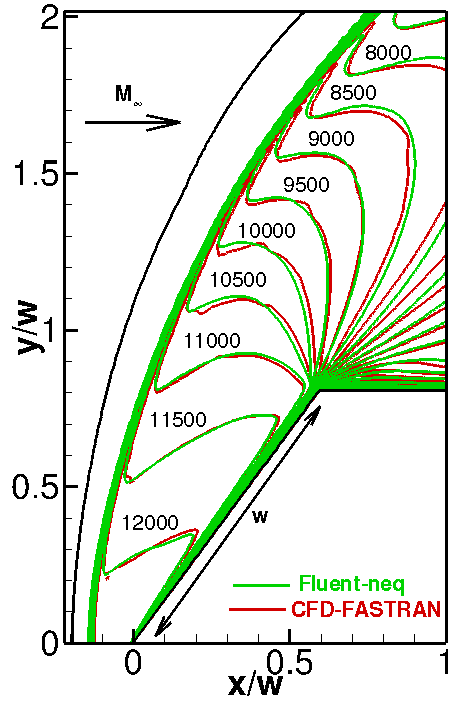
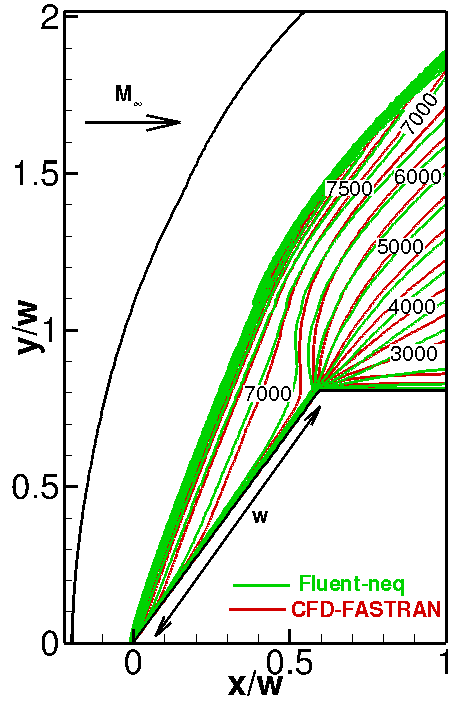
Fig. 2. Temperature isolines without (left) and with (right) dissociation.
The numerical solutions with different (Arrhenius and Park) chemical reaction rate constants are compared in Fig. 3. The only difference between these models is that the Park model uses the geometric average of the translational and vibrational temperatures instead of the translational temperature. As a result, chemical reactions become slower; therefore, the temperature behind the shock and the stand-off distance increase (see Fig. 3, right). This comparison allows us to conclude that the model of chemical reactions is an important factor affecting the numerical solution.

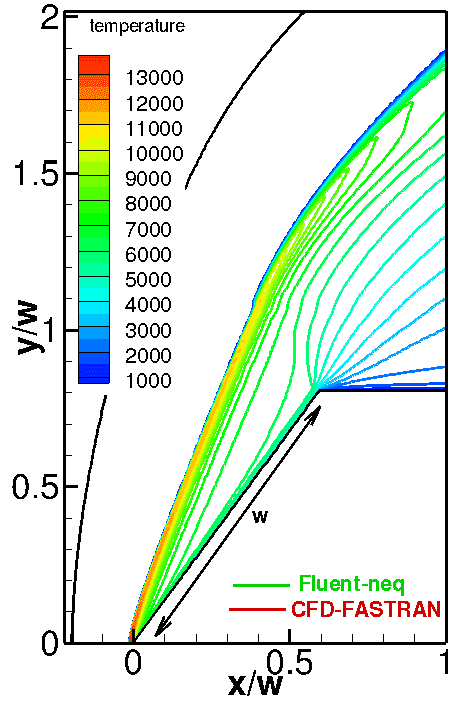

Fig. 3. Comparison of computations with different chemical models: Arrhenius (top-left) and Park (top-right) models. Temperature profiles along the stagnation line are given in the bottom figure.
The full-length paper will present the numerical method and results of simulations in more detail. Additional models of chemical reactions will be also considered and compared with those presented in this abstract. A comparison with the results of the DSMC modeling [5] and experimental data [4] will be performed.
References
- R. Millikan, D. White, Journal of Chemical Physics, Vol. 39, No. 12, 1963, pp. 3209-3213.
- C. Park, Progr. in Astronautics and Aeronautics. Vol. 96, AIAA, New York, 1985, 511-537
- Ye. Bondar, N. Gimelshein, S. Gimelshein, M. Ivanov, I. Wysong. Proc. Of 24th RGD, Vol. 762, 2005, pp. 607-613.
- H. Hornung, G. Smith, Vol. 93, Pt. 2, 1979, pp.225-239.
- Y. Bondar, G. Markelov, S. Gimelshein, M. Ivanov. J. of Thermophysics and Heat Transfer. 20(4), 2006, p. 699-709.

