Inside supersonic nozzles with strong flow confinement due to thick boundary layers, recompression of the flow often occurs in a series of shocks so called shock train, Matsuo et al. 1999. In previous work the authors showed that a shock train inside a rectangular nozzle can be transformed into a single normal shock wave by means of boundary layer bleed through a circumferential normal slot, see Fig. 1, Weiss and Olivier, 2014.
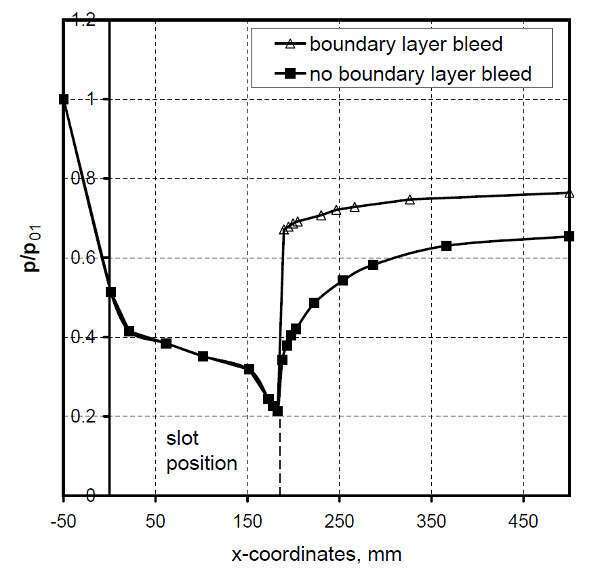
Figure 1. Normalized wall pressure in a rectangular nozzle with and without boundary layer bleed
One of the crucial parameter of the bleed system is the width of the slot. It has to be wide enough to permit sufficient boundary layer bleed. Initially, the necessary slot width was determined experimentally.
In order to improve the understanding of the interaction between the shock wave and the bleed slot, two dimensional numerical calculations were carried out, see Fig. 2
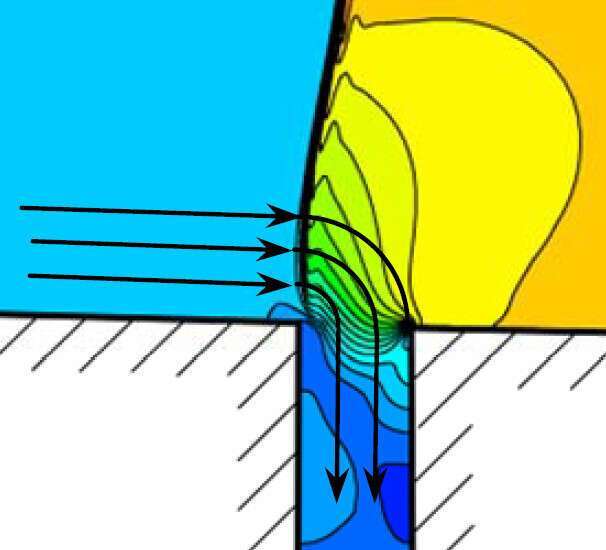
Figure 2. Static pressure distribution at bleed slot Ma∞ = 1.8, slot width 1.5 mm
For a Mach number of Ma = 1.8 the slot width is varied between 0.5 mm, 1.2 mm, 1.5 mm and 2.0 mm. In all four cases, the back pressure at the outlet boundary of the flow domain is increased until the shock wave is located at the upstream side of the bleed slot, see Fig. 2. All remaining geometric and flow parameter are constant. The influence of the slot width onto the shape of the shock wave is discussed as well as the two dimensional static pressure distributions downstream of the shock wave.
Based on these calculations a simple analytical model is derived by which the minimal width of the bleed slot can be estimated, see Fig. 3. The model uses pressure and velocity values and geometric parameters.
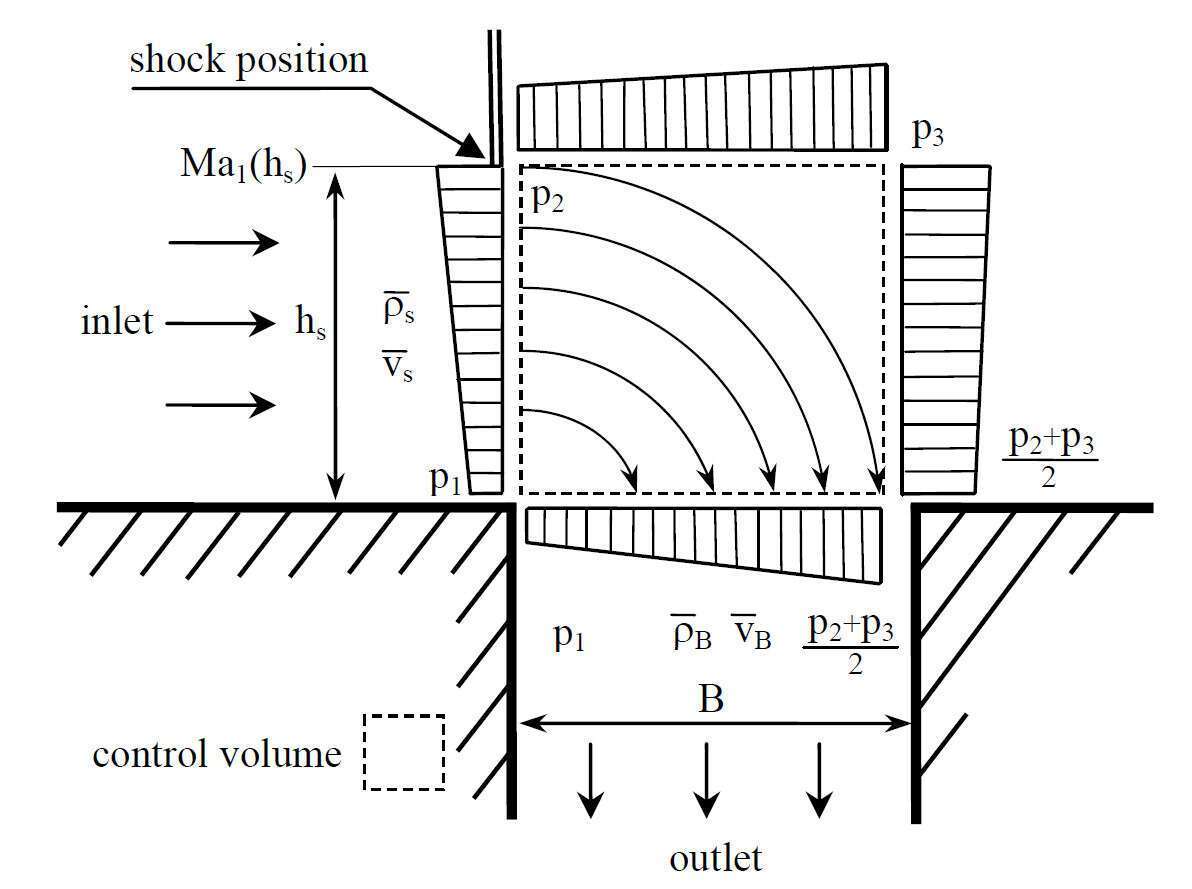
Figure 3. Sketch of simplified flow filed near the bleed slot
Figure 1 also shows, due to the transformation of the shock train into a single shock by means of boundary layer bleed the maximum static pressure gradient greatly increases. Likewise the total pressure downstream of the shock system; measured at x = 500 mm. However, the improved static and total pressure recovery coincide with mass flow losses, which must be taken into account in order to evaluate the usefulness of boundary layer bleed.
Therefore, the maximum static pressure gradient of the shock train and the single shock wave are weighted with the mass flow downstream of the bleed slot respectively. The same method is applied for the total pressure. From the ratio of the mass flow weighted pressure recovery the usefulness of the boundary layer can be derived. This analysis is carried for three Mach numbers Ma∞ = 1.45, Ma∞ = 1.65 and Ma∞ = 1.85.
References
Matuso, K, Miyazato, Y, and Kim, HD, (1999) Shock train and pseudo-shock phenomena in internal gas flows. Progress in Aerospace Sciences 35, 33-100
Weiss, A. and Olivier, H. (2014) Shock boundary layer interaction under the influence of a normal suction slot, Shock Waves 24, 1, 11-19

