On the premise of continuous assumption, the inviscid compressible flows with shocks can be described by the classic Euler equations. For decades, researchers have tried to design variable accurate shock-capturing schemes to solve Euler equations. Finite difference methods and finite volume methods are representative among them. Generally speaking, when constructing a finite volume/difference scheme for solving fluid dynamic problems, one has the option of choosing an upwind method or a centered one, each with its own advantages and drawbacks. Upwind methods try to construct a numerical scheme based on physical sense and the specific eigenstructure of concerned problems have to be solved. When applied to solve conservational equations (e.g. the classic Euler equations) with more than one characteristic value, local Riemann problems have to be solved to determine the cell interface fluxes. The Godunov method [1] is the forerunner of such schemes and is widely used in shock simulations now. For the purpose of bypassing local Riemann problems at the discontinuities of the cell interfaces, a family of central schemes has been constructed by integrating over the Riemann fans, such that the eigen-structures of the concerned problem need not to be solved and the problem can be solved in a straightforward manner as a black box by the central schemes. The first-order Lax-Friedrichs [2] scheme is the pioneer of such central schemes. Compared with the canonical upwind scheme of Godunov, the first-order LxF scheme is a Riemann-solver-free scheme. Its numerical dissipation is so large that the shock discontinuities and rarefaction tips will be seriously smeared out when applied to shock simulations. A straight forward high-order extension of the LxF is the well known Nessyahu and Tadmor [3] scheme whose general idea is to replace the first-order piecewise constant solution distribution embedded in the LxF scheme with the van Leer’s [4] MUSCL-type piecewise linear second-order approach.
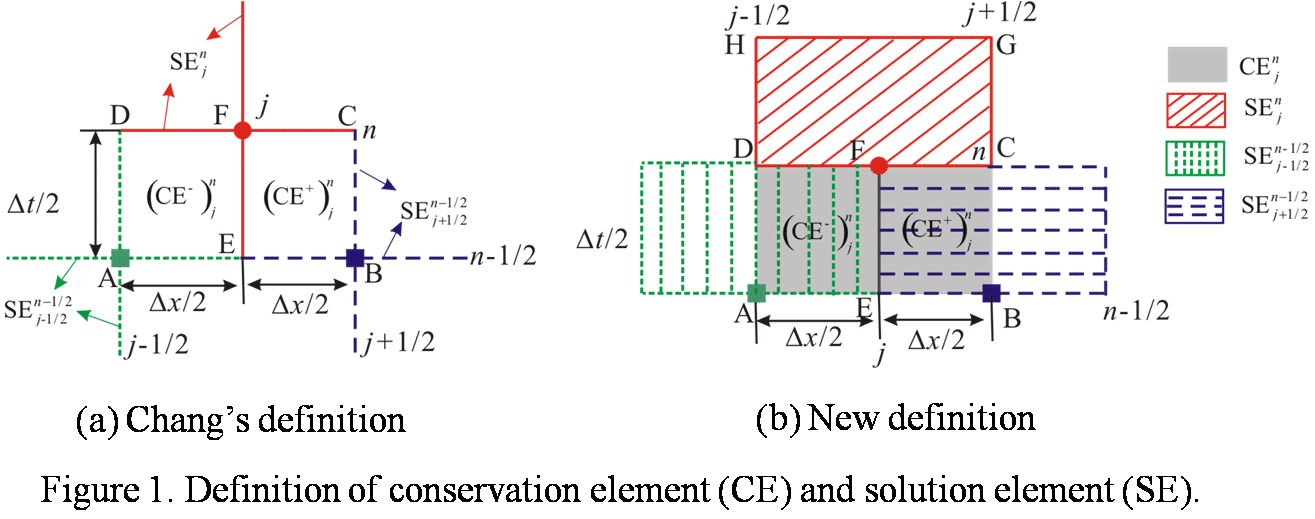
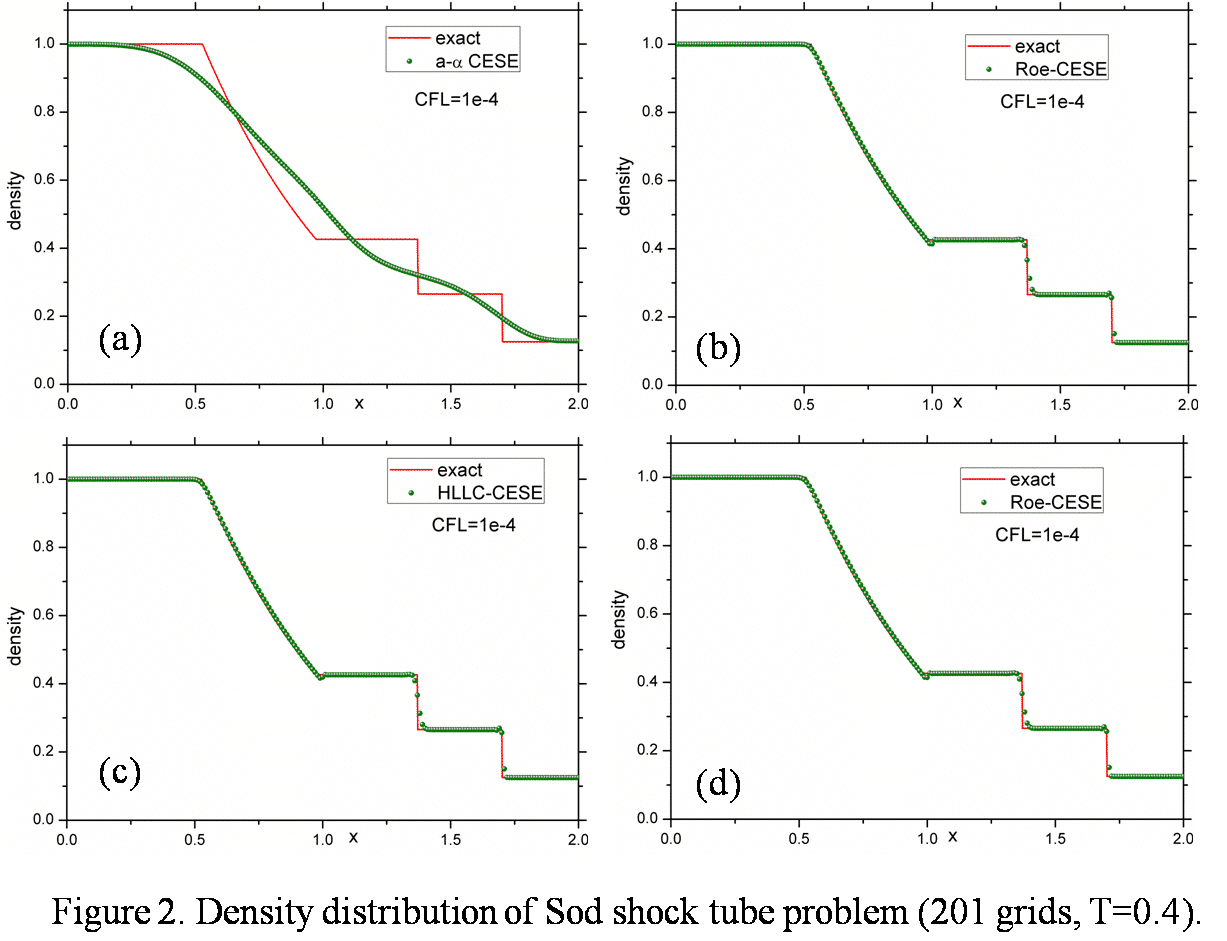
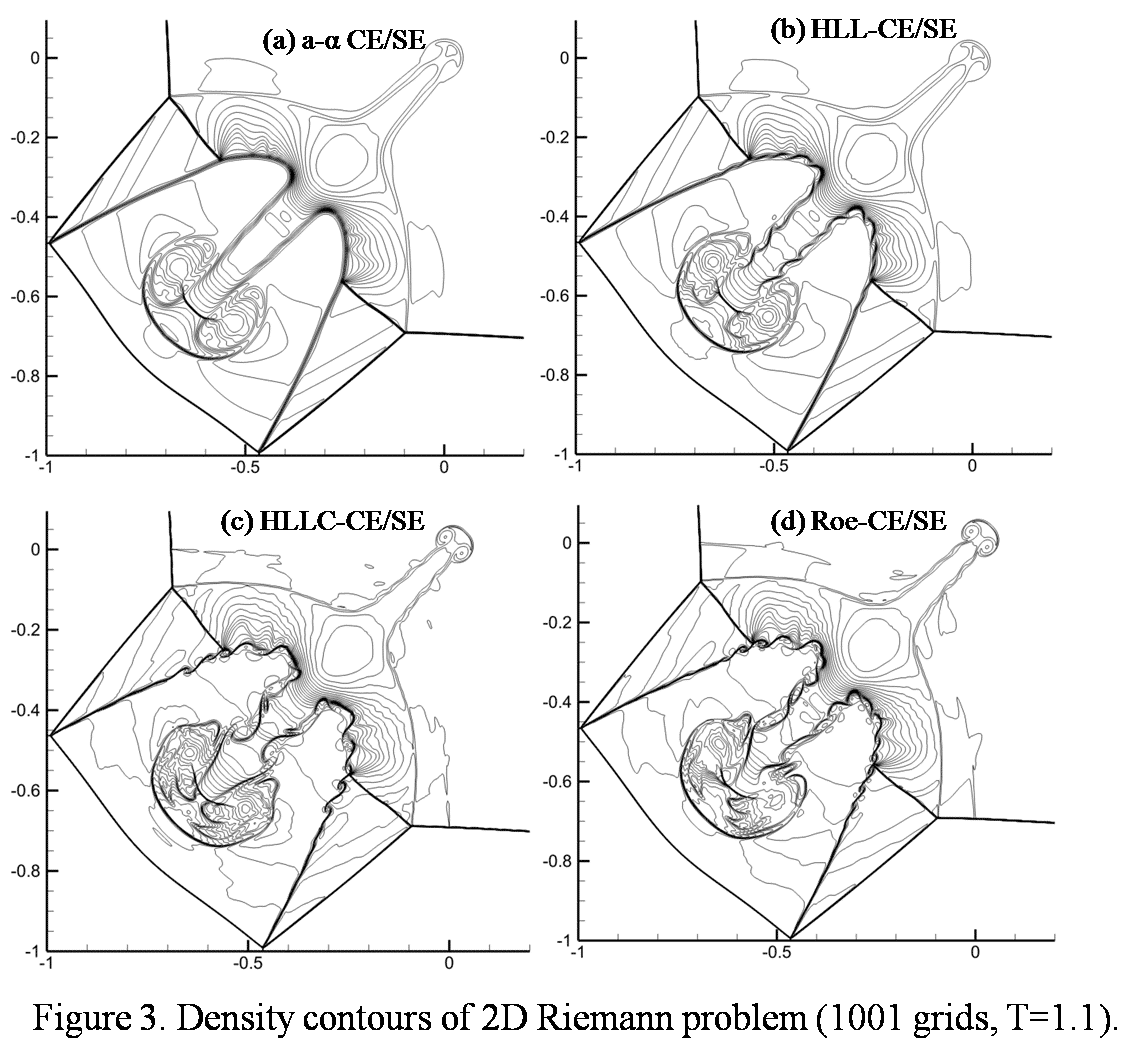
The second-order Space-Time Conservation Element and Solution Element (CE/SE) method, proposed by Chang [5], is a unique centered method. The concept and the start point of the CE/SE method are very different from conventional central methods. In this method, space and time are treated unified. When generating the mesh, space and time are discretized simultaneously, and the solution is updated in a staggered way in the time direction. For each solution point, a conservation element (CE) and a solution element (SE) are defined as shown by Fig. 1(a). When constructing the numerical scheme, the flux conservation is enforced on each CE, and the flux on the boundary of CE is calculated by the Taylor expansion in corresponding SE. In present study, we construct a family of robust and accurate characteristic CE/SE schemes by using the core idea of the original CE/SE method. The definition of CE retains the same as that used by Chang. Nevertheless, the definition of SE is different, as shown in Fig. 1(b). Imposing the conservation law on (CE+)jn and (CE-)jn, two equations were derived. Solving the two equations, we can easily get the time marching schemes of mesh variables and spatial derivatives. From Fig. 1, we can see that the inner boundary of CEjn (EF) is no longer affiliated to SEjn but is located between SE(j-1/2, n-1/2) and SE(j+1/2, n-1/2) in the new definition. As a result, the flow across EF is discontinuous, local Riemann problem must be solved to calculate the flux through EF. In present study, the well known Harten, Lax and van Leer (HLL) Riemann solver [6], contact discontinuity restoring HLLC Riemann solver [7] and mathematically rigorous Roe Riemann solver [8] are adopted. The upwind procedure (local Riemann solver) breaks the space-time inversion invariance of the original scheme, so that the new scheme can be directly applied to capture discontinuities without spurious oscillations. In addition, the present method maintains low dissipation in a wide range of CFL number (from 1e-4 to 1). Furthermore, we extend the new CE/SE schemes to two-dimension. Extensive numerical examples are carried out to demonstrate the robustness of the present method. Fig. 2 shows the numerical results of 1D Sod shock tube problem, it is observed that when the CFL number reduces to 1e-4, the `a-α` CE/SE scheme becomes very dissipative, but the characteristic CE/SE schemes retain good resolution. Fig. 3 shows the numerical results of a 2D Riemann problem simulated by 1001 grids. The characteristic CE/SE schemes capture the Kelvin–Helmholtz instability which is lost in the result derived by `a-α` CE/SE scheme. Indeed, by running this problem on a larger mesh with a conventional scheme, one can see this instability emerging. More detail and more numerical examples will be shown in the full paper and presentation.
Reference
[1] S.K. Godunov, A Finite Difference Method for the Numerical Computation of Discontinuous Solutions of the Equations of Fluid Dynamics, Mat. Sb. 47(1959) 271-306, in Russian.
[2] K.O. Friedrichs, P.D. Lax, Systems of Conservation Equations with a Convex Extension, Proc. Nat. Acad. Sci. 68 (1971) 1686-1688.
[3] H. Nessyahu, E. Tadmor, Non-Oscillatory Central Differencing for Hyperbolic Conservation Laws, J. Comput. Phys. 87 (1990) 408-463.
[4] B. van Leer, Towards the Ultimate Conservative Difference Scheme, V. A Second Order Sequel to Godunov’s Method, J. Comput. Phys. 32 (1979) 101-136.
[5] S.C. Chang, The Method of Space-Time Conservation Element and Solution Element-a New Approach for Solving the Navier-Stokes and Euler Equations, J. Comput. Phys. 119 (1995) 295-324.
[6] A. Harten, P.D. Lax, B. van Leer, On upstream differencing and Godunov-type Schemes for Hyperbolic Conservation Laws, SIAM Rev., 25 (1983) 35-61.
[7] E.F. Toro, Restoration of the Contact Surface in the Harten-Lax-van Leer Riemann Solver, Shock Waves, 4 (1994) 25-34.
[8] P.L. Roe, Approximate Riemann Solvers, Parameter Vectors, and Difference Schemes, J. Comput. Phys. 43 (1981) 357-372.