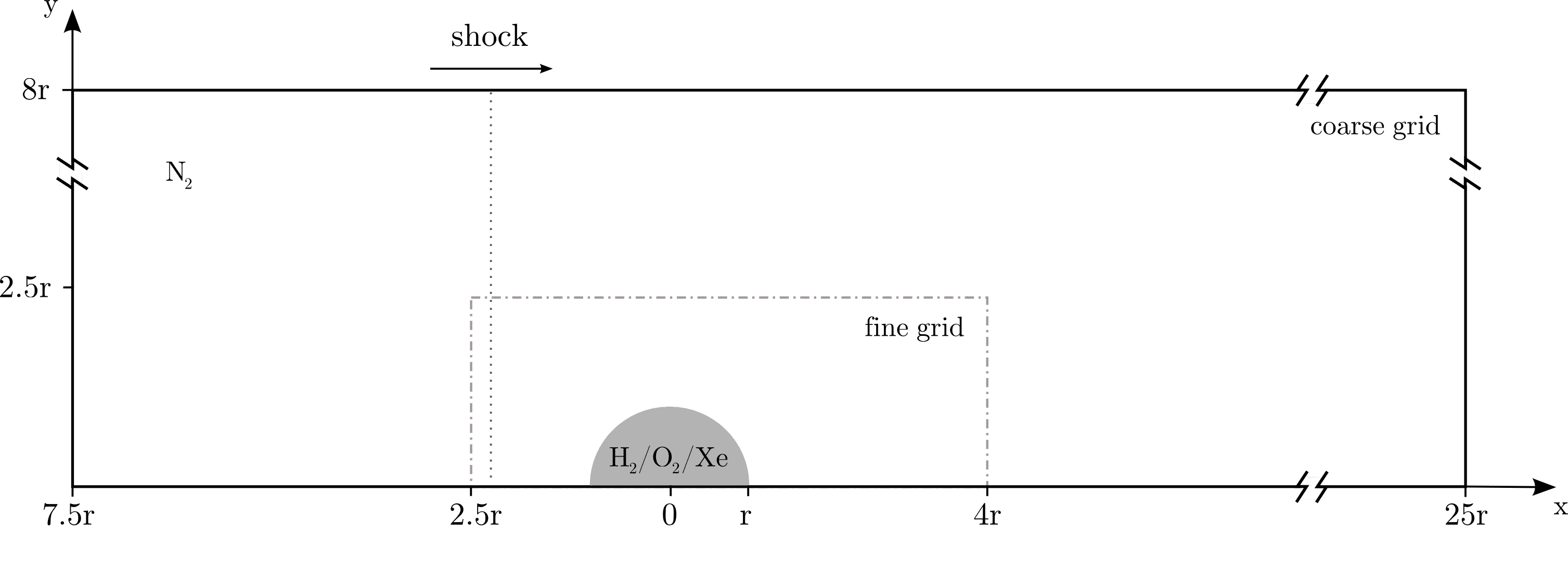
We present numerical results of two-dimensional simulations of a reacting shock-bubble interaction (RSBI) including detailed chemistry. The setup consists of a gas bubble, filled with an ignitable heavy gas, surrounded by an inert light gas. Figure 1 shows a schematic of the computational domain. The bubble gas contains H2, O2 and Xe in a stoichiometric composition with 0.30 / 0.15 / 0.55 mass fractions. The inert gas Xe increases the density of the bubble compared to the surrounding gas N2, resulting in an Atwood number of A = 0.476. The present RSBI setup is based on the experimental setup of a RSBI by Haehn et al. [1]. The shock wave propagates through the domain rightwards and compresses the bubble gas. The difference in the acoustic impedance between the bubble and the surrounding gas causes shock focusing at the downstream pole of the bubble, leading to a spot of high pressure and temperature, which ignites the gas mixture. Furthermore, the shock-bubble interaction induces Richtmyer-Meshkov instability (RMI) at the material interface. Hence, with this setup the interaction of shock-induced RMI and chemical reaction processes can be investigated.
In many reactive flows, such as supersonic combustion, the rapid and efficient mixing of fuel and oxidizer is crucial as the detention time of the mixture in the combustion chamber is only a few milliseconds [2]. RMI promotes mixing by baroclinic vorticity generation and can therefore enhance the burning efficiency of supersonic combustion engines [3].
The increase of temperature and pressure in the shock focusing point can ignite the gas mixture. The resulting reaction wave propagates either with subsonic (deflagration) or with supersonic (detonation) speed through the fluid. As the different reaction branches of H2-O2 combustion are highly pressure sensitive, the reaction wave type depends on the strength of compression and therefore on the shock Mach number. Low compression leads to deflagration dominated by H, O and OH radicals, higher compression induces detonation initiated by HO2 and H2O2.
In the present investigation the full set of compressible, reacting, multicomponent Navier-Stokes equations is solved. 2nd-order Strang time splitting [4] is used to separate the stiff source term from the Navier-Stokes equations. This results in a system of partial differential equations and a system of stiff ordinary differential equations. The latter is solved with the 5th-order backward differentiation formula [5]. The hyperbolic Navier-Stokes flux is discretized by an adaptive central-upwind 6th-order weighted essentially non-oscillatory (WENO-CU6) scheme [6]. The time integration is realized by 3rd-order total variation diminishing Runge-Kutta scheme [7]. The detailed O’Conaire reaction mechanism [8], containing nine species and 19 intermediate reactions, is used to model the chemical reaction rates.
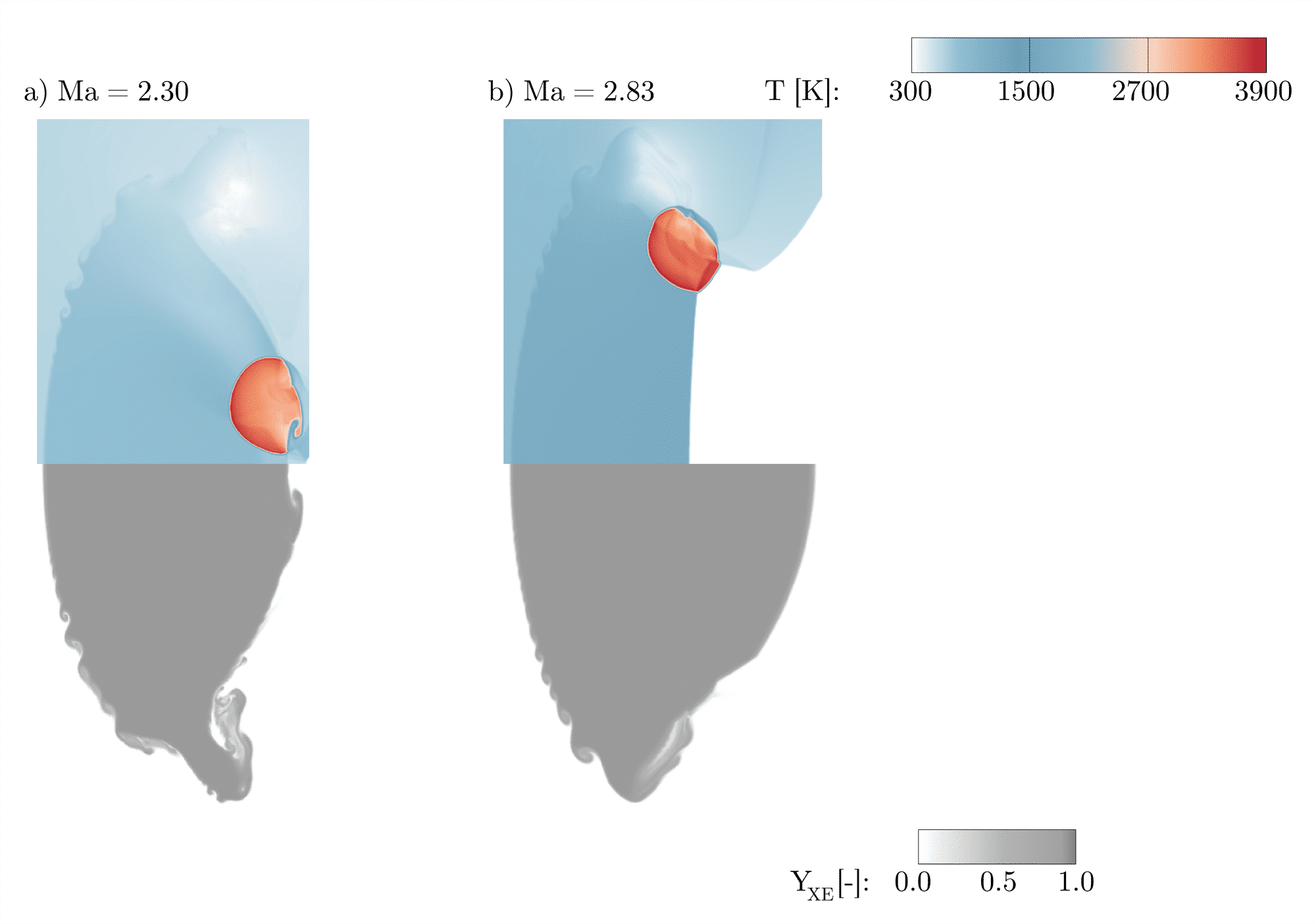
In our study the variation of the shock Mach number between Ma = 1.5 and Ma = 3.0 covers three conditions: no ignition, deflagration and detonation. A weak shock wave associated with a weak compression leads to no ignition within the timeframe of the simulation. Raising the shock Mach number causes higher compression and an increase in temperature and pressure, leading to an ignition at the downstream pole of the bubble followed by a subsonic reaction wave. A further increase induces detonation of the mixtures even before the shock is focused in the downstream pole of the bubble. Figure 2 shows the reaction wave after the detonation at two different shock Mach numbers. The ignition point moves upstream as the shock Mach number is increased. Mixing and the evolution of instabilities are highly affected by the propagation speed, the type of reaction wave and the location of ignition. In the deflagration regime, the chemical reactions have only a weak influence on fluid mechanical instabilities as the characteristic chemical reaction time scale is small compared to the characteristic hydrodynamic time scale. Hence, the bubble evolves very similar as in the non-reacting case. In contrast to the deflagration wave the detonation wave rapidly propagates through the bubble and strongly affects the following evolution of the instabilities and mixing.
For a quantitative analysis the total mixing rates (TMR) and the normalized bubble diameter (NBD) will be presented to confirm the different evolutions depending on the type of reaction wave and therefore on the shock Mach number. The rapid combustion caused by the detonation accompanied by the fast expansion of the burned bubble gas leads to a sudden increase of the NBD. The same development is observed for the TMR: The mixing rate rises rapidly while the detonation wave propagates through the fluid. For the deflagration case, NBD and TMR increase monotonically while the reaction wave propagates through the bubble gas.
References:
[1] Haehn, N., Ranjan, D., Weber, C., Oakley, J., Rothamer D. and Bonazza,R. (2012). Reacting shock bubble interaction. Combustion and Flame, 159(3):1339–1350.
[2] Yang, J., Kubota, T., and Zukoski, E. (1993). Applications of shock-induced mixing to supersonic combustion. AIAA Journal, 31:854–862.
[3] Marble, F., Zukoski, E., Jacobs, J., Hendricks, G., and Waitz, I. (1990). Shock Enhancement and Control of Hypersonic Mixing and Combustion. In AIAA 26th Joint Propulsion Conference, Orlando, FL.
[4] Strang, G. (1968). On the Construction and Comparison of Difference Schemes. SIAM Journal on Numerical Analysis, 5(3):506–517.
[5] Brown, P. N., Byrne, G. D., and Hindmarsh, A. C. (1989). Vode: A variable-coefficient ode solver. SIAM Journal on Scientific and Statistical Computing, 10(5):1038–1051.
[6] Hu, X. Y., Wang, Q., and Adams, N. A. (2010). An adaptive central-upwind weighted essentially non-oscillatory scheme. Journal of Computational Physics, 229(23):8952.
[7] Gottlieb, S. and Shu, C.-W. (1998). Total variation diminishing Runge-Kutta schemes. Mathematics of Computation, 67:73–85.
[8] Ò Conaire, M., Curran, H., Simmie, J., Pitz, W., and Westbrook, C. (2004). A comprehensive modelling study of Hydrogen oxidation. International Journal of Chemical Kinetics, 36:603–622.

