Cellular and spin detonation in 3D channels of different shapes is investigated. The study is carried out numerically using the original software package in which the modified S.K. Godunov`s method for multi-block grids is implemented and parallelized using MPI. This paper presents the results of calculations performed on 1000-10000 CPU cores of the MSU supercomputer "Lomonosov" with computational meshes consisting of 0,1 to 10 billions of cells.
Processes observed in experiments with the initiation and propagation of divergent detonation in a narrow gap between plates have been simulated. The detonation wave is formed in a tube adjoined at a right angle, and this gap passes therein through a circular hole. Due to the complexity of the flow region`s geometry, the actual phenomenon is of a three-dimensional nature. But the flow inside the tube is close to one-dimensional, and the size of the interplate gap is sufficiently small. Therefore, transverse waves propagating in the direction normal to the plates are absent, and the two-dimensional divergent cellular detonation is realized within the gap. Fig. 1 shows for comparison (a) the experimental pattern and (b) the calculated pattern for wakes of triple points. One can see the good consistency of two-dimensional model for description of the process.

Fig 1. Traces of triple points besides the diverging cylindrical detonation wave. The results of the experiment (a) and calculation (b)
Three-dimensional cellular detonation in semi-closed channels with fixed square, rectangular, circular and elliptical cross sections has been obtained. Formation of cellular structure was spontaneous due to one-dimensional initial distribution of gas-dynamic parameters in channels. The length of the channels was equal to 1 m, linear size of computational cells in all cases did not exceed 0.1 mm.
In all cases the detonation of a stoichiometric propane-air mixture at rest under normal conditions was studied. It was considered that the channel has a flat closed end, near which in the zone of 3 cm width initiation of detonation occurs due to instantaneous uniform electric discharge. By the statement of the problem the flow initially is one-dimensional, the parameters of which depend only on the longitudinal coordinate z. Due to the instability and the rounding errors at machine precision the one-dimensional detonation wave is transformed to cellular at some distance. The local maximum pressure map constructed inside the channel during the calculation formed a numerical three-dimensional soot foot diagram similar to those in simulations of two-dimensional cellular detonation.
The calculation scheme and software package were verified by transition from 3D to 2D geometry. Calculations have shown that transition to regular two-dimensional cellular detonation is realized, but, however, the critical interplate gap in third dimension, which divides regimes with clear or highly diffuse soot foot diagrams, appeared very small.
For channels that are significantly different from the flat two-dimensional, principally three-dimensional cellular structure of detonation was obtained with transverse waves propagating in the plane of the section. The shape of the traces on the surface of the channel is different from the rhomboid, but reminds periodically structure, although quite “chaotic”. Fig. 5 for example, illustrates the numerical soot foot diagram on the surface of the channel of square section 10x10 mm obtained in numerical simulation.

Fig. 2. Numerical soot foot diagram on the surface of the channel of square section
Three-dimensional cellular detonation in a circular and elliptic channels was obtained (Fig. 3, 4).
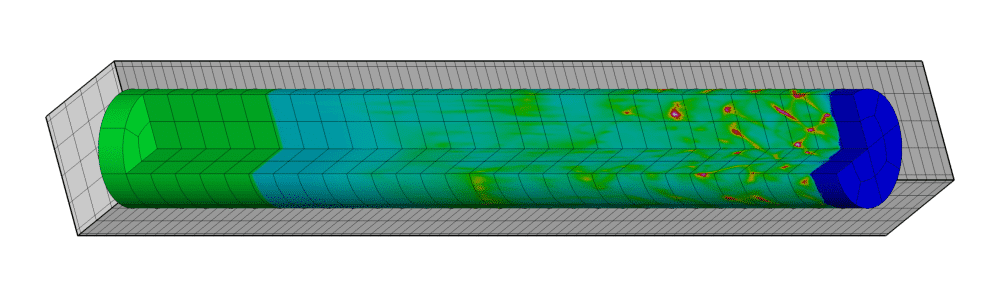
Fig. 3. The emergence of three-dimensional cellular detonation in the channel of circular section
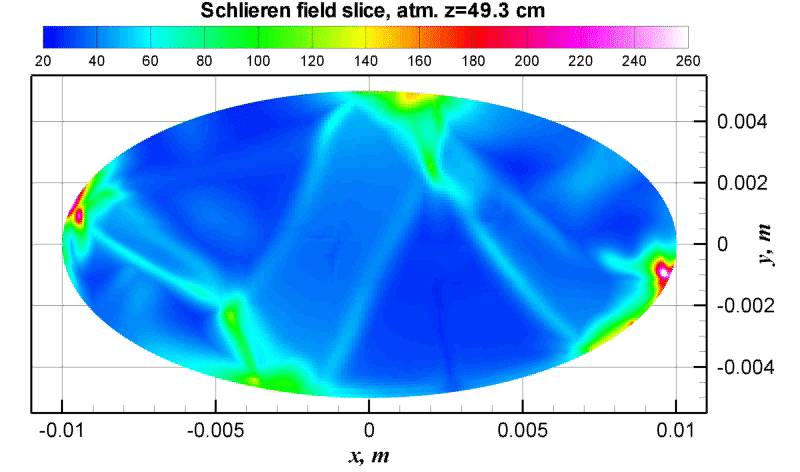
Fig. 4. Slice z=0.5 m of three-dimensional numerical soot foot diagram obtained for the elliptic channel
For circular channel the critical diameter was found, leading to spin detonation if below. The spin detonation was obtained in calculations without any external impact, with strongly 1D initial distribution, and due to instability of 1D flow. Fig. 5 illustrates the initial phase – irregular and undeveloped spinning detonation at the distance 22 cm. Fig. 6 corresponds to developed and stationary spinning detonation in the same calculation at the distance 75 cm.
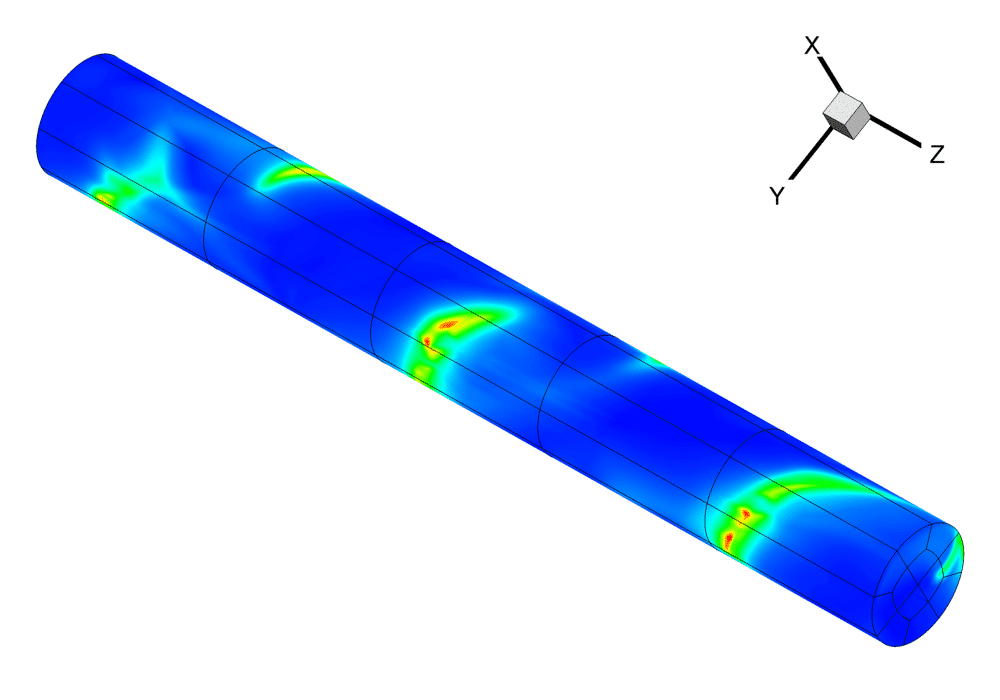
Fig. 5. Emergence of three-dimensional spin detonation in the channel of circular section

Fig. 6. Developed three-dimensional spinning detonation in circular channel
Spin detonation transition from 6-mm diameter channel to the channel of larger or smaller diameter through a short section of conical shape was investigated. Calculations have shown that there is a range of values of diameter such that the spin detonation maintains or recovers. Fig. 7 is presented to compare 3D views of different channels fragments with numerical soot foot diagrams upon spin detonation exiting the channel of 6-mm diameter and entering channels with diameters 4, 5, 8 and 10 mm. For 10 mm the spin detonation mode is destroyed. For 8 mm the spin detonation recovers, passing a phase with wave pattern close to two-head spin detonation. For 5 mm spin detonation also persists. The case 4 mm is on the border of the mentioned range. It corresponds to uncertain mode, but also with rotation which goes in opposite direction.
To analyze the patterns of flow that emerge in calculations, the sweeps of lateral channel surface coated with soot foot diagrams were visualized (Fig. 8). Developed spin detonation can be identified by periodically repeating oblique stripes.




Fig. 7. Channels fragments with numerical soot foot diagrams upon spin detonation exiting the channel of 6-mm diameter and entering channels with diameters 4, 5, 8 and 10 mm

Fig. 8. Sweep of lateral surface with numerical soot foot diagram obtained for the channel widened from 6 to 8 mm
The work was supported by the Russian Science Fund (Grant No. 14-19-01759).

