Investigations on the mechanism of flame acceleration and deflagration-to-detonation transition for combustible gas are of significance in the field of explosion safety. Reactive Navier-Stokes equations, including the advection-diffusion term with non-stiffness and the reaction term with stiffness, are used to describe the propagating process of flame acceleration. Multi-time scale gives rise to the difficulties in direct numerical simulation of DDT process. On discretizing the time, explicit scheme requires very small time step, while huge nonlinear equations to be solved are encountered in implicit scheme. Constructing a stable numerical scheme with large time step is meaningful, which computational cost in compressible reactive Navier-Stokes systems can be dramatically saved.
Integration factor (IF) method discretizing time for the classical non-linear partial differential equations not only enhances the computing stability but also reduces the time direction numerical errors from the high order derivatives[1-4].Zhang et al proposed an implicit integration factor (IIF) method to solve PDE systems with stiff source terms[5]. In present paper, we extend the method to reactive flow Navier-Stokes equations and investigate the mechanism of the flame acceleration and the transition of deflagration to detonation. Krylov implicit integration factor is utilized to discretize time for solving systems with both stiff and non-stiff terms. High order WENO scheme based on finite difference is used to discretize the advection terms, and central difference scheme to discretize the diffusion terms. Hence, the relatively larger time step can decrease the total number of time steps. The large sparse matrix caused by the implicit scheme is mapped to the lower dimensional Krylov subspace which can also save computational cost.
We use the presented method to effectively simulate laminar flame acceleration in two-dimensional channel with non-slip wall. Figure 1 shows the variation of temperature in the process of flame propagation. It can be seen that initially heat expansion from reaction renders flame front go forward, which leads to flow in unreacted gas. Due to the non-slip wall boundary condition, the flow in the middle of tube is fast and the flow near walls is slow. Hence, the flow in front of flame forms a gradient from middle location to boundary. As flame propagates into the gas, flame front curves and take on a shape like a finger. Then the area of flame surface and the rate of energy release increase, which make flame accelerate rapidly. Figure 2 shows the position of the flame tip versus time. It shows that the laminar flame accelerates exponentially as the flame front constantly stretches, which is in good agreement with the result in [6].
The present method to deal with the stiffness offers a new idea for direct numerical simulation of flame acceleration and deflagration-to-detonation transition. Moreover, it can also be extended to solve the three-dimensional Reactive Navier-Stokes equations with detailed reactions.

Fig.1 Laminar flame acceleration
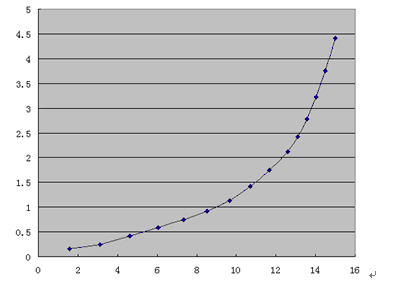
Fig.2 Scaled position of the flame tip versus scaled time
Reference
[1] G Beylkin, J M Keiser, L Vozovoi. A new class of time discretization schemes for the solution of nonlinear PDEs. Journal of Computational Physics, 1998. 147: 362-387.
[2] S M Cox, P C Matthews. Exponential time differencing for stiff systems. Journal of Computational Physics, 2002. 176: 430–455.
[3] A-K Kassam, L N Trefethen. Fourth-order time stepping for stiff PDEs. SIAM Journal of Scientific Computing, 2005. 26: 1214–1233.
[4] Y Maday, A T Patera, E M Ronquist. An operator-integration-factor splitting method for time-dependent problems: application to incompressible fluid flow. Journal of Scientific Computing, 1990. 5: 263-292.
[5] Q Nie, Y T Zhang, R Zhao, Efficient semi-implicit schemes for stiff systems. Journal of Computational Physics, 2006. 214: 521-537.
[6] V Bychkov, V Akkerman, G Fru, A Petchenko, L Eriksson. Flame acceleration in the early stages of burning in tubes. Combustion and Flame, 2007. 150: 263-276.

