Experimental Analysis of Shock Stand-off Distance in Hypersonic Flows over spherical Bodies

Shock stand-off distance is a basic parameter associated with detached shocks in hypersonic flows over blunt bodies. In spite of the considerable amount of previous work done on this aspect, there is still no universal methodology to predict the shock stand-off distance for a particular body geometry and flow conditions. A major breakthrough was provided by Van Dyke in 1958 when he proposed a numerical method to predict the shock stand-off distance over a spherical body in high speed flows. In 1964, Lobb experimentally proved Van Dyke`s theory and gave a mathematical expression for the same. In 2000, Olivier conducted a theoretical analysis on the same problem over spherical bodies and formulated a different expression for the shock stand-off distance. In 2014, Zander et al. published results of similar work carried out in high velocity flows of the order of 9 km/s. In this paper, the results of experimental work conducted on spherical bodies, facing moderate to high enthalpy flows (upto 2 km/s) , for which data does not exist in open literature, is presented. These results were compared with that of Lobb and Olivier. Computational analysis was also carried out in commercial CFD packages, Fluent and HiFun.

The experiments were conducted in hypersonic shock tunnel (HST2) and free piston shock tunnel (FPST) of Laboratory for Hypersonic and Shock Wave Research, Indian Institute of Science. HST2 is a conventional shock tunnel with a 2 m long driver, 5.12 m long driven and 50 mm inner diameter. It can work in a Mach number range of 6 - 12, Reynolds number range of 0.3 - 6 million/m and a maximum stagnation flow enthalpy of 3 MJ/kg. The effective test time in this tunnel is 700 - 800 µs. FPST consists of a 10 m long compression tube, and a 5 m long driven tube of 50 mm inner diameter. It can generate flows of stagnation enthalpy as high as 25 MJ/kg. The effective test time in this tunnel is around 500 µs. The experiments conducted for this work had nominal free-stream Mach numbers of 6, 8, and 11. Air and CO₂ were used as the test gases in this study. The free-stream flow conditions for these cases are given in Table 1.

Schlieren photography was employed to visualize the flow in front of the test models and the shock stand-off distance was discerned from the images using edge detection technique. These experiments were carried out on 3 different spherical models of radii 25 mm, 40 mm, and 50 mm. Each model comprised a hemisphere and a cylindrical after body of 20 mm length. These models were fabricated from Duralumin 2014. Figure 1 shows the test models used in this work.

Figure 2 shows a schlieren image of the 25 mm model in HST2 for a typical Mach 6 run. From the experimental data, it was observed that the shock stand-off distance increases during the flow build up, remains more or less constant during the test time, and increases further during the flow termination.

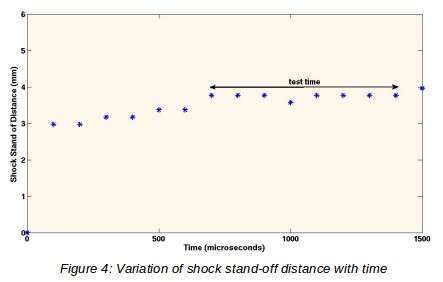
Figure 3 shows the schlieren images of the shock stand-off distance variation with time for the same Mach 6 run. Figure 4 shows the variation of value of shock stand-off distance with time for the same run. The average value for this run was found to be 3.77 mm from the analysis of the images. The experimental data was compared with that of Lobb and Olivier and a good match within 5% was obtained. For the same flow conditions, Lobb predicted it to be 3.96 mm and Olivier estimated it at 3.97 mm. Figures 5 and 6 show the results of the computations carried out using HiFun for the same free-stream conditions, for inviscid and viscous models respectively. Shock stand-off distance from this analysis was found to be 3.9 mm for both cases. The detailed experimental, analytical and computational results will be provided in full paper.

References

1. M.D. Van Dyke, “The supersonoic blunt-body problem – review and extension”, AIAA Journal, Vol. 25, No. 8, pp 485-496, 1958.

2. R.K. Lobb, “Experimental measurement of shock detachment distance on spheres fired in air at hypervelocities”, The high temperature aspects of hypersonic flow (Nelson ed.), Pergamon press, pp 519-527, 1964.

3. H. Olivier, “A theoretical model for the shock stand off distance in frozen and equilibrium flows”, Journal of Fluid Mechanics, Vol. 413, pp 345-353, 2000.

4. F. Zander, R.J. Gollan, P.A. Jacobs. R.G. Morgan, “Hypervelocity shock stand-off on spheres in air”, Shock Waves, Vol. 24, pp 171-178, 2014.