In February 2013, a meteorite dropped in Chelyabinsk, Russia. Its mass was about 10kt, the size was approximately 17-20m, and the speed was nearly 19km/s. This meteorite induced a large-scale disaster, mostly by breaking window glasses, due to the shock wave impact. More than 1,000 people were injured over a region of 180 km in the north-south and 80 km in the east-west direction. A similar meteorite entry reported before was the Tunguska event in 1908.
It is critical to predict and understand that how the shock wave induced by the fall of a meteorite, and this shock wave affects the ground dozens of kilometers away, for the crisis management and disaster measure. One method is to calculate the pressure using the technique of computational fluid dynamics (CFD). However, to calculate numerical simulation of such a phenomenon, it is necessary to evaluate shock wave pressure in far field properly together with the meteorite. This imposes a challenge in CFD. Consider a meteorite of tens of meters in diameter. The grid spacing in CFD should be the order of a few meters, say 1m, then ten thousands of cells are necessary to capture the shock wave10 kilometers ahead in a 1-D problem. It is prohibitive for three dimensions.
A subgrid-scale modeling of the meteorite motion in the large space is required.
The SOVA code that was originally developed for small particles [1,2] can be potentially used for this purpose. However, the quantitative evaluation of the far-field shock wave pressure is not yet investigated.
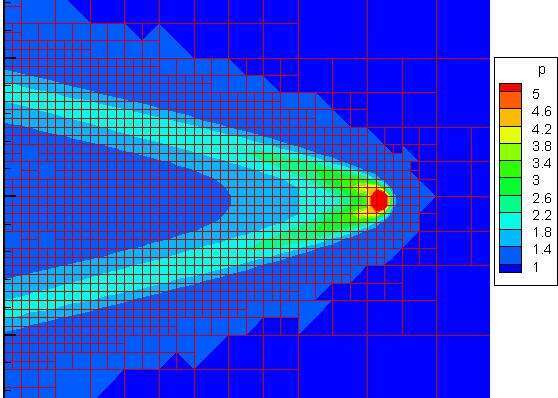
Fig.1 shock wave pressure distribution by small meteorite model
In this study, we treat the small meteorite as a subgrid-scale particle with a finite volume as shown in Fig.1. The Subgrid Closure Model (SCM method, [3]) was used to handle the movement of subgrid-scale particle while maintaining the entropy condition.
We use a Lagrange-Remap Method in the numerical analysis method. In the Lagrange-step, the Euler coordinate system grids are regarded as the initial state of the Lagrangian particles in the Lagrange frame, and the physical quantities of the solid (a small meteorite) and gas (air) are averaged in the cell. Next, pressure and velocity at the grid interface are calculated by the Riemann solver. Interactions in the cell are evaluated by SCM method. In this study, the volume for the solid phase assumed to be constant, and the momentum change is obtained by considering the air drag. When these calculations are finished, the conservative quantities in the Lagrange coordinate system are remapped back to the Euler coordinate system. And the above procedure is repeated.
The long-term aim of this study is to predict the pressure on ground induced that the meteorite entry as in the Chelyabinsk event. Therefore, we quantitatively record and evaluate the pressure change at a long distance of 100 times of the diameter of the meteorite. It is found that the pressure rise at the far-field is very sensitive to the modeling of the small meteorite. More discussion on the modeling of the meteorite will be reported in the full paper.
REFERENCES
- V.V.Shuvalov, Multi-dimensional hydrodynamic code SOVA for interfacial flows:Application to the thermal layer effect. Shock Waves 1999; 9:381-390
- O.P. Popova et al., Chelyabinsk airburst, damage assessment, meteorite recovery and characterization, Science 342, (2013)
- M. Sun, A thermodynamic and dynamic subgrid closure model for two-material cells, Intl. J. for Numr. Methods in Fluids, 73, pp. 130–151, 2013

