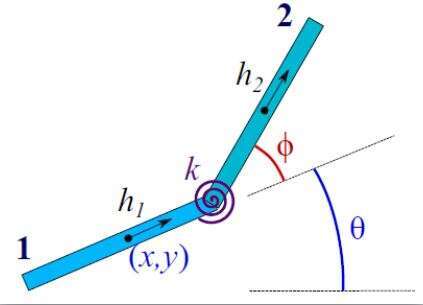
One of the most efficient actuation methods of robotic microswimmers for biomedical applications is by applying time-varying external magnetic fields. In order to improve the design of the swimmer and optimize its performance, one needs to develop simple theoretical models that enable explicit analysis of the swimmers dynamics. This work studies the dynamics of a simple microswimmer model with two magnetized links connected by an elastic joint, which undergoes planar undulations induced by an oscillating magnetic field. The nonlinear dynamics of the microswimmer is formulated by assuming Stokes flow and using resistive force theory to calculate the viscous drag forces. Key effects that enable the swimmer to overcome the scallop theorem and generate net propulsion are identified, including violation of front-back symmetry. Assuming small oscillation amplitude, approximate solution is derived by using perturbation expansion, and leading-order expressions for the swimmer`s displacement X or V are found for given swimmer`s parameters. An ultimate optimal choice of swimmers parameters and actuation frequency is found, for which the average swimming speed V attains a global maximum. Finally, the optimal performance values are compared to reported experimental results of magnetic microswimmers.