Consider a shock tube configuration with a sharp transition between a wide driver segment and a narrower driven segment. The flow commencing upon the rupture of the diaphragm that separates the two segments is studied both numerically and by analytic modeling. This analysis is aimed in particular at understanding the converging flow through the sharp area contraction, paying special attention to the separation bubble that evolves as the flow negotiates the sharp corner at the entrance to the driven segment. For a high driver-to-driven pressure ratio (in the example of Fig. 1 below it was 100) the large-times flow at the entrance to the driven segment is quasi-steady. The separation bubble downstream of the corner seems to produce a choked vena-contracta flow with a smooth transition from subsonic to supersonic velocity (Fig. 1). It is this flow that drives the shock wave into the long driven segment. The numerical study was performed on an axisymmetric configuration with an area ratio 36 and initial pressure ratio 100, first by solving the Euler equations (using the GRP method), then by a commercial code (FLUENT) based on the Navier-stokes equations. An example of the flow Mach number map obtained by the GRP code is shown in Fig. 1. On this color map, the solid line indicated a sonic (M=1) surface. The separation bubble is also visible on this map.
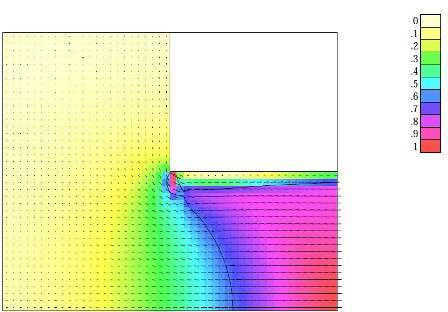
Figure 1. Mach number flow map near the driver-driven interface.
While CFD solutions do provide a detailed view of the flow field, it is generally difficult to get an understanding of the observed phenomena in terms of well-known concepts of classical fluid dynamics. Here we seeks such insight by resorting to analytic modeling (see [1]), where the large-time flow model is based on simple 1-D fluid-dynamical “building blocks”, such as steady quasi-one-dimensional isentropic flow, or simple 1-D waves – centered rarefaction, shock discontinuity, and contact discontinuity.
REFERENCE
1. J. Falcovitz, O. Igra, Model for shock interaction with sharp area reduction, Proc. IMechE Vol. 222 Part G: J. Aerospace Engineering, pp. 789-800, 2008.

