Electron Energy-Loss Spectroscopy (EELS) Calculation in Finite-Difference Time-Domain (FDTD) Package: EELS-FDTD

Nicolas Large Department of Chemistry, Northwestern University, Evanston, Illinois, USA Yang Cao Department of Physics and Astronomy, Rice University, Houston, Texas, USA Alejandro Manjavacas Department of Physics and Astronomy, Rice University, Houston, Texas, USA Mingliang Zhang Department of Materials Science and Engineering, Stanford University, Stanford, California, USA Daniel Park Department of Chemistry, Northwestern University, Evanston, Illinois, USA Jessie Ku Department of Chemistry, Northwestern University, Evanston, Illinois, USA Mohammad Shahjamali Department of Chemistry, Northwestern University, Evanston, Illinois, USA Shan Wang Department of Materials Science and Engineering, Stanford University, Stanford, California, USA Chad Mirkin Department of Chemistry, Northwestern University, Evanston, Illinois, USA George Schatz Department of Chemistry, Northwestern University, Evanston, Illinois, USA Peter Nordlander Department of Physics and Astronomy, Rice University, Houston, Texas, USA

Electron energy-loss spectroscopy (EELS) is a unique tool that is extensively used to investigate the plasmonic response of metallic nanostructures since the early works in the `50s. To be able to interpret and theoretically investigate EELS results, a myriad of different numerical techniques have been developed for EELS simulations: boundary element method (BEM), discrete dipole approximation (DDA), finite-element method (FEM), Galerkin discontinuous time-domain (GDTD) method. Although these techniques are able to predict and reasonably reproduce experimental results, they possess significant drawbacks and are often limited to highly symmetrical geometries, non-penetrating trajectories, free-standing nanostructures, and small nanostructures. Here, we present a novel approach for EELS calculations using the finite-difference time-domain (FDTD) method that goes beyond these limitations.[1] We benchmark our EELS-FDTD implementation by direct comparison with results from the well-established BEM and published experimental results. In particular, we compute EELS spectra for spherical nanoparticles, nanoparticle dimers, nanodisks supported by various substrates, and supported gold bowtie antennas. The flexibility our EELS-FDTD method allows for easily extending to more complex geometries and configurations. To illustrate this we investigate the plasmonic properties of (i) high density sub-10-nm-gap metallic dimers, (ii) periodic arrays of silver and gold nanoparticles, and highly irregular triangular gold nanoframes.[2,3] This implementation can also be directly exported beyond the FDTD framework and implemented within other numerical methods and solvers.

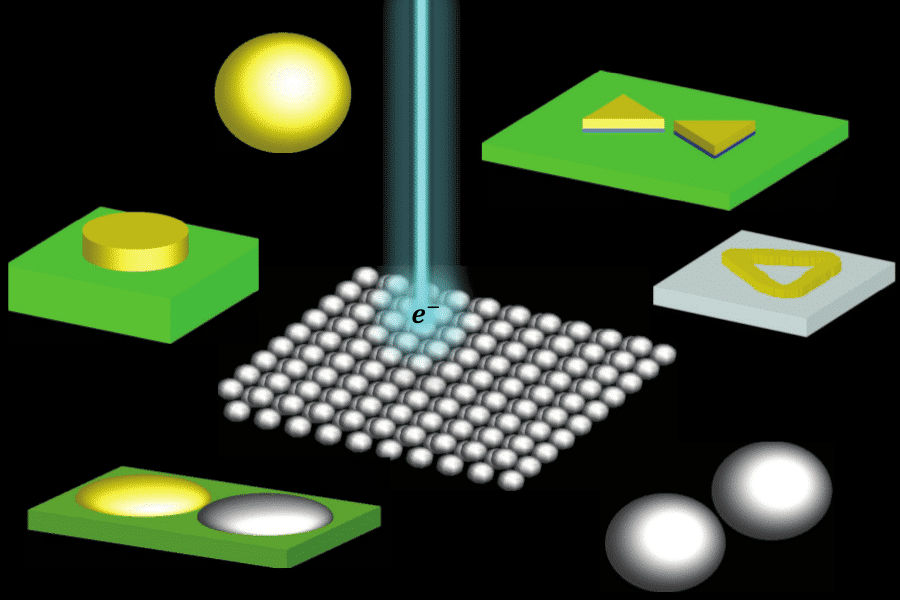
Figure: Schematics of the different geometries investigated using the EELS-FDTD implementation: isolated nanosphere, dimer of nanospheres, supported lithographic hetero-dimers, nanodisk, bowtie-antennas, triangular nanoframes, and nanoparticle superlattices.

References:

[1] Y. Cao, A. Manjavacas, N. Large, P. Nordlander, Electron Energy-Loss Spectroscopy Calculation in Finite-Difference Time-Domain Package, Submitted

[2] M. Zhang, N. Large, A.-L. Koh, Y. Cao, A. Manjavacas, P. Nordlander, R. Sinclair, S. X. Wang, High-Density 2D Homo- and Hetero- Plamonic Dimers with Universal Sub-10-nm gaps, In preparation

[3] M. M. Shahjamali, A. Li, M. Bosman, N. Zaraee, N. Large, D. Park, S. Li, G. C. Schatz, C. Xue, C. A. Mirkin, Optical Properties of Triangular Gold Nanoframes; Experimental and Theoretical Study, In preparation

Nicolas.Large@northwestern.edu