Mechanisms of Second Harmonic Generation in Plasmonic Nanostructures

Second harmonic (SH) generation (SHG) in plasmonic nanostructures originates from the surface of centrosymmetric metals where inversion symmetry is broken. The interest in that topic stems from the high sensitivity of the SHG to geometrical changes in the system. For example, it was reported that SHG can be enhanced by near-field coupling between a resonator at the fundamental frequency and one at the second harmonic, building together a double-resonance antenna (DRA). However, the underlying physical mechanisms leading to strong SHG with a DRA are still to be understood, which is important to achieve full control over the SH radiation.

In this presentation, we provide a full understanding of the mechanisms that lead to SHG in multi-resonant plasmonic structures. By combining both surface integral equation simulations and experiments on aluminum plasmonic nanostructures, we investigate the SHG modulation from DRAs with a broad variety of geometries. For this purpose, the long bar L₂ of a DRA is optimized and fixed at 160 nm, while the short bar L₁ is varied from 20 to 200 nm. We clearly observe that the SH intensity is maximum when the short bar has also a maximum scattering cross section in the linear regime at 400 nm. The SH intensity observed in that case is twice that when the short bar does not have a resonance at 400 nm. The corresponding SH near-field distribution confirms that the near-field of the quadrupolar SH sources from the long bar L₂ excite the dipolar mode of the short bar L₁, Fig. 1(b). If the short bar L₁ is increased, it becomes out of resonance and the SH intensity decreases dramatically, indicating the role of energy transfer between both bars, Fig. 1(c). SHG increases again when the short bar L₁ is such that the structure becomes symmetric, L₁=160 nm in Fig. 1(c). The agreement between calculations (red line) and experiments (blue line) is excellent, Fig. 1(c).

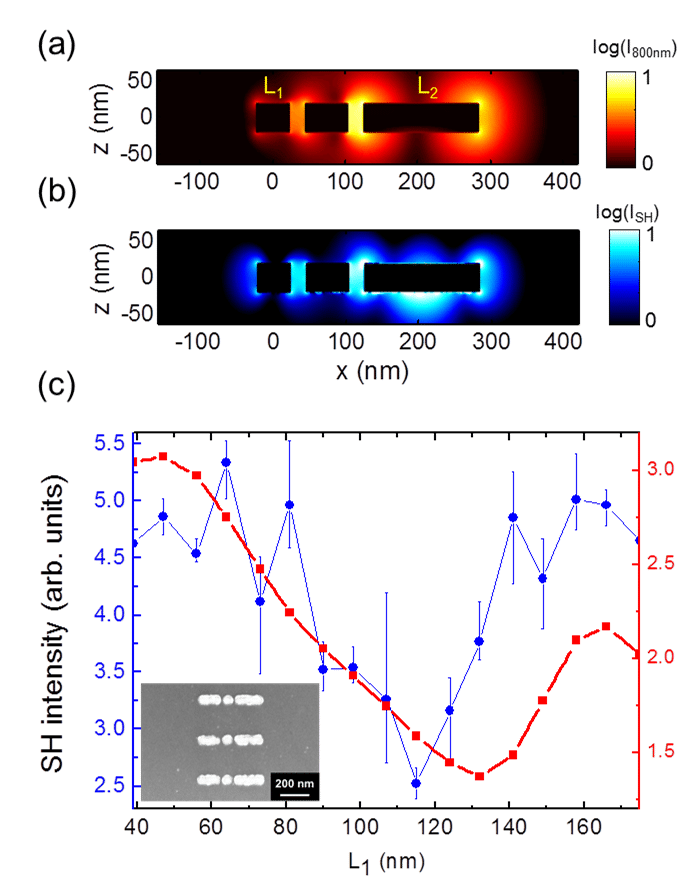
Fig. 1:    Near-field distributions of the DRA with L₁=47nm. (a) Fundamental intensity (b) second harmonic intensity (c) SH intensity versus different L₁ cases.

kuang-yu.yang@epfl.ch