
Self-Formation of Parity-Time Symmery in Lossy Media
In optics, parity-time (PT) symmetry on light propagation occurs only when the refractive index distribution of loss/gain media obeys a relation of n(x) = n*(-x) [1]. The real index should be an even function of position whereas the imaginary be odd, therefore a π/2 phase-shift between the real and imaginary indices is crucial for PT symmetry [2].
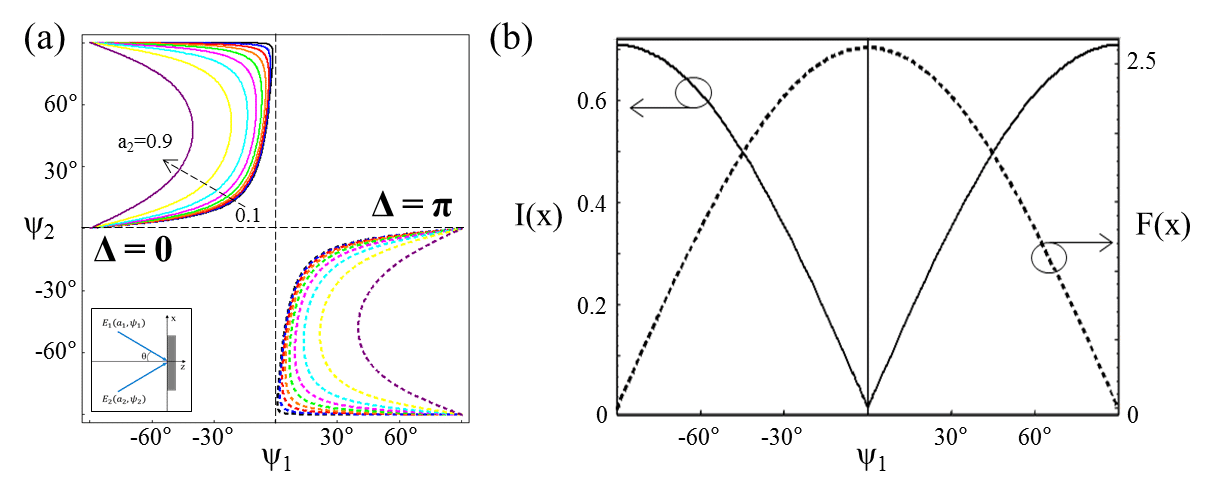
We propose a mechanism for self-formation of an exact π/2-shift in complex media by employing a polarization interference on azo-chromophore films. When an azo-polymer film is illuminated by interference of two polarized beams, a surface-relief grating structure formed by the gradient force F(x) of polarization [3] contributes to the real-index distribution while the intensity distribution I(x) to the imaginary-index one. If we define α and β for the phases of F(x) and I(x), Δ ≡ α – β, the phase difference between F(x) and I(x). Δ is a function of ai and ψi (i = 1, 2), where ai is ellipticity and ψi polarization angle of the two interference beams as represented in inset of Fig. (a). Δ should be 0 or π for PT symmetry. Figure (a) shows parameter combinations for Δ = 0 or π with a1 = 0 and 0 < a
[1] C. M. Bender, S. Boettcher, "Real spectra in non-Hermitian Hamiltonians having PT symmetry," Phys. Rev. Lett. Vol. 80, 5243 (1998).
[2] H. Hodaei, M. Miri, M. Heinrich, D. Christodoulides, M. Khajavikhan, "Parity-time-symmetric microring lasers," Science, Vol. 346, 975 (2014).
[3] W. Joo, C. Oh, Y. Han, “Influence of the Backbone on Photoinduced Birefringence in a Poly ( malonic ester ) Containing p -Cyanoazobenzene,” J. Phys. Chem. B, Vol. 106, 5378 (2002).
choloong.hahn@gmail.com
Powered by Eventact EMS