Second Harmonic Generation from Arrays of Nonlinear Metamaterial Nanocavities

Igal Brener CINT, Sandia National Laboratories, Albuquerque, New Mexico, USA Salvatore Campione CINT, Sandia National Laboratories, Albuquerque, New Mexico, USA Alexander Benz CINT, Sandia National Laboratories, Albuquerque, New Mexico, USA Arvind Ravikumar CINT, Sandia National Laboratories, Albuquerque, New Mexico, USA Sheng Liu CINT, Sandia National Laboratories, Albuquerque, New Mexico, USA Emil Kadlec CINT, Sandia National Laboratories, Albuquerque, New Mexico, USA John Klem CINT, Sandia National Laboratories, Albuquerque, New Mexico, USA Michael Sinclair CINT, Sandia National Laboratories, Albuquerque, New Mexico, USA

Second harmonic generation (SHG) is a nonlinear process traditionally carried out using nonlinear crystals. Intersubband transitions (IST) in semiconductor quantum wells (QW) offer second order nonlinearities that are orders of magnitude higher but require complicated coupling schemes. Planar metamaterials resonators fabricated on top of these samples can be used to couple light efficiently, and increase the conversion efficiency. [1,2]

Our semiconductor samples consist of multiple periods of asymmetric double-QWs of In0.53Ga0.47As/Al0.48In0.52As, on top of an InP substrate. Two intersubband transitions were designed at 30 THz (fundamental) and 60 THz (second harmonic). Transmission through the QW stack was measured in a wedge configuration and is shown in Fig. 1(a): the dips correspond to absorptions arising from the 1>2 and 1>3 ISTs. Arrays of gold split ring resonators (SRR) supporting the same resonances at 30 and 60 THz were patterned on top of the sample using e-beam lithography and liftoff. A schematic of the SRR is shown in Fig. 1(b) together with an illustration of the two supported resonances. A comprehensive theoretical analysis of this structure, discussing both linear and non-linear processes, has been presented elsewhere [1].

The sample was pumped at ~30 THz (~10mm), and the emission at the SH frequency was measured using a calibrated InSb detector. Low intensities were pumped using a grating tunable, CO2 laser while higher intensities were attained using an optical parametric amplified laser system. Figure 1(c) depicts the power measured at the SH versus pump intensity on a log-log scale. For low pump powers we observe a quadratic dependence on pump power whereas for high pump powers we witness a transition to linear dependence (Fig. 1(c)). The conversion efficiency reaches a value of ~0.36% for an intensity of ~14 kW/cm2. This value is remarkable considering the very short (~λSH/10) path-length through the active QW medium. We will also discuss how to manipulate the phase front of the second harmonic emitted radiation.

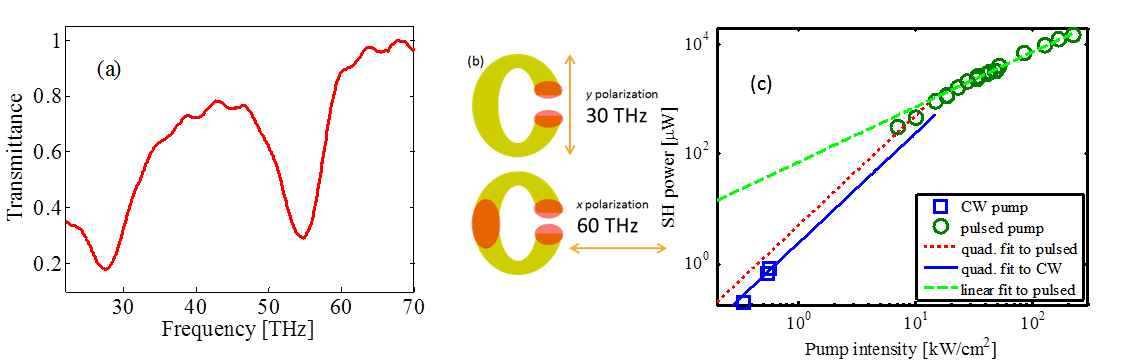
Fig. 1. (a) Transmission of the QW stack, measured in the wedge configuration. The dips correspond to the ISTs transitions. (b) Main resonant modes of the SRR (yellow ‘C’). The red regions correspond to field ‘hot spots’ - locations where the out of plane electric field is enhanced. (c) Log-log plot of the SH power versus pump intensity. ‘Pulsed pump’ data is on-resonance for λ=10.15 µm; ‘CW pump’ data is for λ=10.22 µm.

Fig. 1. (a) Transmission of the QW stack. (b) Main resonant modes of the SRR (yellow ‘C’). The red regions correspond to field ‘hot spots’. (c) Log-log plot of the SH power versus pump intensity.

References

[1] J. Lee et al, Nature 511, 65–69 (2014).

[2] S. Campione et al Appl. Phys. Lett. 104, 131104 (2014) 131104.

ibrener@sandia.gov









Powered by Eventact EMS