
Robust Point-to-Point Near-Field Lensing by a Double-Negative Single-Interface
Typical working near-field imaging schemes employ a scanning apparatus, e.g. a sensing tip whose finite size and scattering efficiency determine resolution. Using a double-negative (DNG) medium slab as a non-scanning perfect-resolution imaging device, while a conceptually pioneering idea, has thus far proved inapplicable due to very high sensitivity to intrinsic DNG media loss and the ultra-narrow band of the effect.
Here we propose a lensing configuration which can in principle overcome these difficulties, with potential for actual application. It is realized by a simple single-interface between a regular dielectric (DPS) containing the source (imaging object) and a DNG metamaterial containing an ideal detection element (drain) – where a perfect image is formed (Fig. 1a). The unexpected robustness of this configuration is arrived at by modal, scattering (reflection and transmission), and excitation (Green) studies. Perfect point-to-point lensing is maintained even under realistic material loss and/or excitation frequency offsets, mainly since the optical transfer function (Fig. 1b-d red) remains a spatial all-pass filter (rather than a low-pass as with the DNG slab lens, green).
The modal lensing mechanism relies solely on excitations of an ‘improper’ (double-diverging) Brewster mode in between the source and image planes, whose flat dispersion (Fig. 1e) allows for its excitation and subsequent reflectionless transmission at any spatial frequency.
Practical limitations to resolution are concerned with two controllable factors: the quality and density (pixel-size) of detection elements, and the exposure time necessary for a desired resolving power (perfect focusing only forms at the stationary limit).
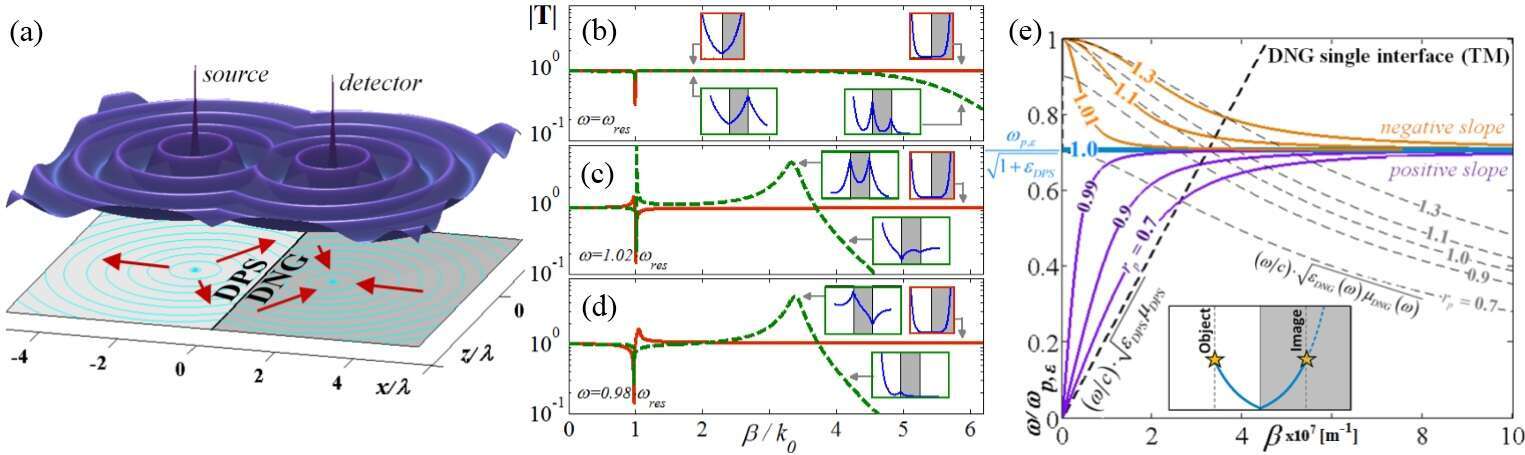
Fig. 1. (a) Stationary field solution for a point-source excitation perfectly „copied“ by a lossless DNG-DPS single-interface onto a point-drain (power direction, red). (b-d) Amplitude transmission vs. propagation constant β for lossy single-interface (red) and slab (green) lenses at several frequencies (inset: field profile at indicated points). (e) Brewster mode (inset) dispersion curve at matched (μDPS/εDPS=μDNG/εDNG, blue) and mismatched conditions (rp=ωp,μ/ωp,ε values indicated). ε,μDNG=1–ω2p,ε,μ/ω(ω+i·ωτ,ε,μ), ε,μDPS=1, ωp,ε=1.37·1016, ωres=ωp,ε/(1+εDPS)1/2.
Powered by Eventact EMS