
Quantum Nonlocal Effects in Individual and Interacting Graphene Nanoribbons
We show that doped graphene narrow ribbons support near-infrared plasmons with important quantum nonlocal corrections. Remarkably, the removal of single-atom rows from extended graphene is enough to separate ribbons that strongly interact with incident light.
We show that highly doped graphene ribbons can support surface plasmons at near-infrared frequencies when their width W is in the nanometer range. We rely on a quantum-mechanical approach to the optical response1 that allows us to go beyond a classical local description in order to account for nonlocal and quantum finite-size effects. The latter are important for widths below W~10 nm, as revealed by comparison with classical theory2. In our work, we assess the magnitude of these effects by comparing classical and quantum-mechanical models to describe graphene plasmons.
We also find strong influence of nonlocal effects on the orientation of graphene edges, as well as on the hybridization between ribbon plasmons in dimers and arrays for separations below a few nanometers. Specifically, the orientation of the edges relative to the graphene atomic lattice plays a crucial role, with zigzag edges contributing to damp the plasmons at energies above the Fermi level, due to the participation of electronic edge states. In contrast, armchair ribbons can support well defined plasmons at energies above EF. Remarkably, the removal of a single line of atomic bonds in a ribbon produces a strong plasmon frequency shift, whereas the removal of bonds along an array of lines separated by several nanometers in an extended sheet causes a dramatic increase in the absorption.
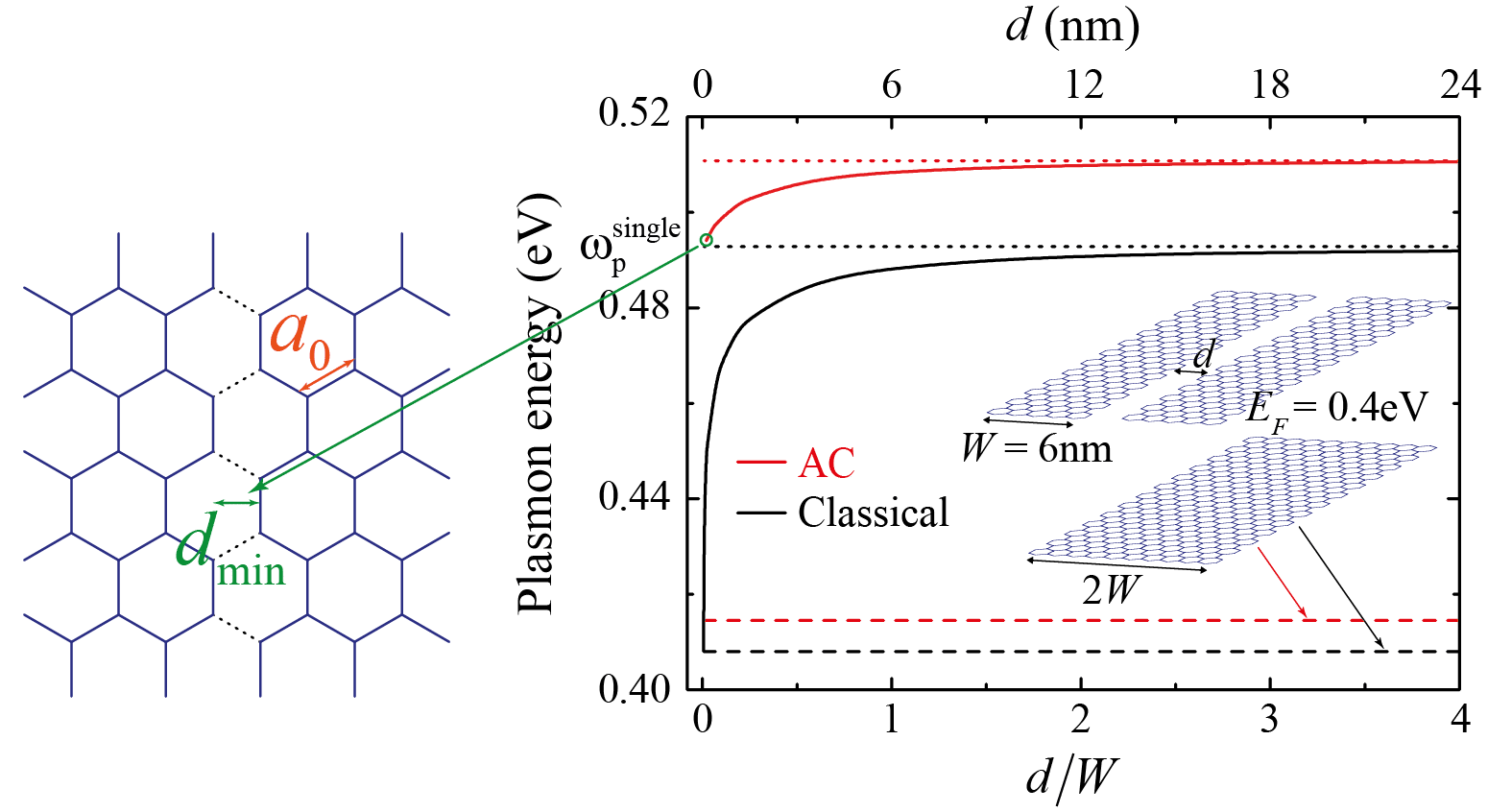
We represent the plasmon peak energies of a graphene ribbon dimer (width W = 6 nm, Fermi energy EF = 0.4 eV, and intrinsic damping of 0.02 eV) as a function of the edge-to-edge distance d using classical and quantum-mechanical (for armchair ribbons, AC) models. The left figure shows the nearest separation dmin = 31/2a0/2 considered for the quantum AC calculations, where a0 = 0.1421 nm is the carbon-carbon bond distance.
[1] S. Thongrattanasiri, A. Manjavacas, and F. J. García de Abajo, ACS Nano 6, 1766 (2012).
[2] S. Thongrattanasiri, I. Silveiro, and F. J. García de Abajo, Appl. Phys. Lett. 100, 201105 (2012).
ivan.silveiro@gmail.com
Powered by Eventact EMS